Изследване на проекции на ръбести тела в системата „СтруниМа“

Д-р Младен Вълков

Institute of Mathematics and Informatics

Bulgarian Academy of Sciences (Bulgaria) (Bulgaria)

Abstract. В системата „СтруниМа“ е изградена функционалност за визуализиране на тримерна квадратна мрежа, чрез която могат да се намират предни и задни проекции на различни ръбести тела – тела, съставени от единични кубчета, или на ръбести тела с върхове, които са върхове и на квадратната мрежа. Също така е изградена и състезaтелна част, чрез която по дадени проекции на стените и ръбовете да се възстанови началното тяло.

Keywords: „СтруниМа“, техническо чертане, проекции, ръбове, стени

Introduction

1.1. Изучаване на проекции на тримерни тела в училище

Изобразяването и изследването на тримерни тела със софтуер е фундаментално в множество индустрии – строителство и архитектура, компютърни игри, виртуална реалност, моделиране на физични процеси и др. С наличието на достатъчен брой софтуери за визуализация на тримерни тела се появява възможността за по-широко изучаване на свойствата им в стандартното образование по математика, както и мултидисциплинарни дейности с предмети като техническо чертане. В България примерите за такива софтуери (AutoCAD, GeoGebra и др.) и приложението им в обучителен процес, включващ дескриптивна геометрия за студенти, са немалко (Zareva, Chehlarova, 2016; Chehlarova, Stanchev, 2001), както има и примери за ученици (Lebamovski, Nikolova, 2019). Въпреки това и изградените множество STEM центрове подобни часове и дейности са рядкост, което има своите последствия върху изграждането на пространствено мислене у учениците.

1.2. Изучаване на проекции на тримерни тела в „СтруниМа“

В системата „СтруниМа“ (https://strunima.valkovbg.com/play-in-browser/) има клас от подтеми, които се базират на изследването на тримерни тела и комбинаторно-геометрични свойства върху тях – симетрия върху тримерна дъска (Valkov, 2024), покрития на тримерна дъска с плочки полимино, изследване на проекции върху тримерна дъска, възли в пространството, усуквания на Конуей и др. Изследването на първа, втора и трета проекция на тела, съставени в тримерна квадратна мрежа, заедно с комбинаторно условие се оказва добро упражнение за развитие на пространственото мислене на учениците.

В темата „Покрития на дъска“ е изработена дъска, разделена на единични квадратчета (кубчета), които могат да бъдат оцветявани или премахвани от дъската. Дъската може да се ротира и да има произволни размери, по-малки от 100. Разработени са две подтеми. Първата е „Проекции на тримерна дъска“ (Valkov, 2024) (фиг. 1):

Фигура 1. Първа, втора и трета успоредна проекция на фигурата, съставена от показаните кубчета – https://strunima.free.bg/CoveringProjections.html

Впоследствие се разработи функционалност, която изследва проекциите на произволно ръбесто тяло върху три проекционни равнини. Може да се достъпи през темата за покрития върху дъска и покриващи многоъгълници (фиг. 2) и след това с промяна на четирите плъзгача да се направи празна квадратна мрежа.

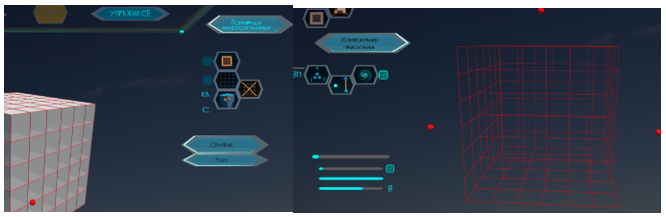
Фигура 2. Достъп и стойности на плъзгачите за направата на мрежа,
в която всички кубчета са изключени

При избирането на кои да е две от червените отсечки се построява връх върху пресечната им точка. От падащото меню под „Свързване“ може да се избере „Многоъгълник“ – след това направените върхове могат да се свързват с множество от многоъгълници, за да се направи тримерно намиращо се в квадратната мрежа (фиг. 3). Чрез четвъртия плъзгач се променя позицията на предния квадрат, като това дава възможност за построяване на върхове във вътрешността на мрежата.

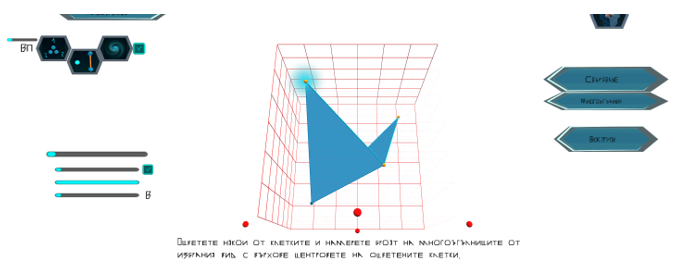
Фигура 3. Построяване на тетраедър върху мрежата

При избиране на „Тримерна конструкция“ от падащото меню до бутона за проверка на проекциите могат да се направят ортогоналните (Elias, 2012) такива, които се наблюдават отляво, отгоре и отпред. Видимите и невидимите ръбове се проектират съответно в оранжев и син цвят, като ако невидим ръб лежи върху видим, се вижда само видимият. Всеки от върховете на ръбестото тяло се проектира върху съответната равнина.

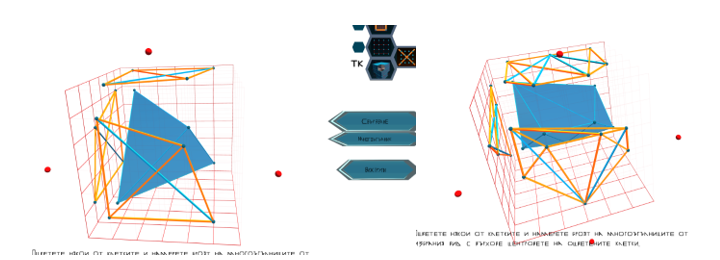
Фигура 4. Построяване на проекции на ръбесто тяло

В системата е изградена серия от състезателни нива, при които са дадени първа и втора проекция на предварително генерирани тела и се изисква от състезаващия се да построи третата проекция на тялото. Тук не е разрешено да се построява тялото във вътрешността на мрежата (т.е. четвъртият плъзгач е скрит). При съставянето на нивата като трудност може да се отбележи използването на проекции, за които има точно едно решение. За останалите е необходимо да се състави алгоритъм, който да определя дали по три дадени проекции съществува тяло, което отговаря на тях, и да се имплементира алгоритъм за това (Dimitrov, 2002; Fang, 2014; Park, Shiratori, Matthews, Sheikh, 2010; Idesawa, 1973; Hoang, 2020; Wei, Yuanjun, 2006).

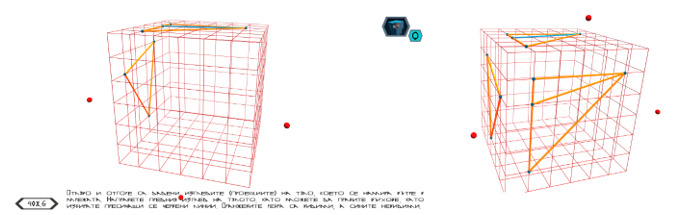
Фигура 5. Начално състояние на състезателното ниво и очаквано решение,

преди да се натисне бутонът за проверка

Проведени учебни часове с изградените дигитални инструменти в системата „СтруниМа“

В STEM кабинета на ППМГ „Нанчо Попович“ се проведоха няколко учебни часа с ученици от V и VII клас, базирани на изследването на проекции на тяло, съставено от кубчета. Задачата се състои в това при дадена тримерна дъска 3х3х3 (фиг. 6.) да се премахне най-големият брой кубчета, така че дъската да запази трите си проекции.

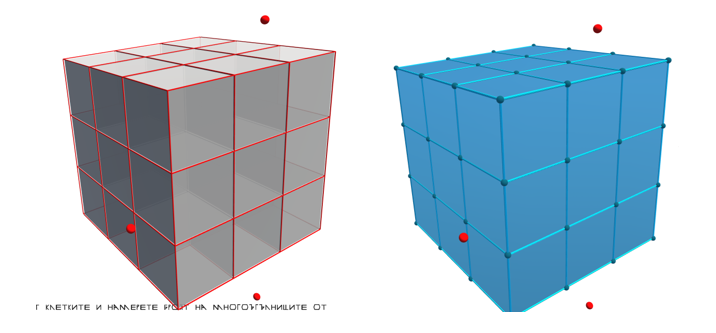
Фигура 6. Ортогонални проекции на куб 3х3х3

Минималният брой оставащи клетки е 9, тъй като трябва да имаме поне една клетка във всеки блок 1х3. Първоначалната реакция на учениците беше, че това не е възможно, докато не се даде пример с първия слой 3х3, от който може да се оставят само трите клетки по диагонала.

Фигура 7. Ортогонални проекции на куб 3х3х3

След намирането на решението за куб 3х3х3 немалко ученици успяха да се справят с минимална помощ със същата задача за куб 4х4х4. Проведените часове могат да се считат за мултидисциплинарна дейност, включваща математика (комбинаторика), техническо чертане и информационни технологии, като софтуерът дава възможност да виждат на всяка стъпка промените по проекциите, както и да изследват самото тяло, съставено от кубчетата в различни ротации. Има разработена функционалност, която позволява изобразяването и на ръбовете на тялото, което при състезателните нива (намиране на тяло, съставено от кубчета по дадени проекции) внася допълнителна трудност.

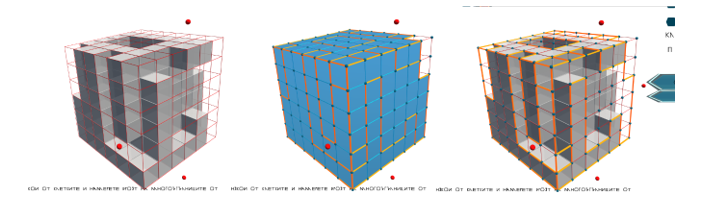
Фигура 8. Проекции с ръбове на тялото, съставено от кубчета

ЛИТЕРАТУРА

Вълков, М. (2024). Централна симетрия върху тримерна дъска, Central symmetry on a 3-dimensional board, 10 години Виртуален училищен кабинет по математика, ISBN 978-954-561-636-5.

Вълкова, Д., Вълков, М. (2024). Използване на системата СтруниМа в обучението по техническо чертане, Автоматизация на дискретното производство, 2, ISSN 2682-9584, mf.tu-sofia.bg/adpmagazine/includes/archive/2024_2.pdf.

Зарева, Ц. (2016). Модел за изучаване на дексриптивна геометрия с динамични конструкции за струденти по архитектура и строителство, БАН, Автореферат.

Зарева, Ц., Чехларова, Т. (2016). Грешки при намиране на равнинно сечение на тяло в аксонометрия и средства за преодоляването им. Педагогически форум, 3.

Лебамовски, П., Николова, М. (2019)., Иновативен подход в обучението по стереометрия в училище с помощта на стереосистема StereoMV, DOI: 10.55630/STEM.2019.0101.

Чехларова, Т., Станчев, Г. (2001). Формиране на умения у студентите за работа с грешки на занятията по АВИТО. В: Научни трудове на ПУ „П. Хилендарски“. 38(2), Методика на обучението, 107 – 112.

Elias, M. (2012). 3D Model reconstruction from vector perpendicular projections, Scientific Monographs in Automation and Computer Science, 1.

Dimitrov, J. (2002). Automatic reconstruction from scanned image of mechanical drawing in axonometry, Annual of the University of Mining and Geology “St. Ivan Rilski”, 44 – 45, part III, Mechanization, electrification and automation in mines, Sofia, 93 –97.

Fang, F. (2014). Algorithms for the Recovery of 3D Objects from 2D Line Drawings, School of Mechanical & Aerospace Engineering, Nanyang Technological University.

Idesawa M. (1973). A system to generate a solid figure from three view, Bulletin of the JSME, 16(92).

Hoang, L. (2020). 3D Solid Reconstruction from 2d Orthographic views, Mixed Reality and Three-Dimensional Computer Graphics, DOI: 10.5772/intechopen.91977.

Park, H. S., Shiratori, T., Matthews, I., Sheikh, Y. (2010). 3D Reconstruction of a Moving Point from a Series of 2D Projections.

Wei, L., Yuanjun, H. (2006). 3D model retrieval based on orthogonal projecitons, Computer Aided Design and Computer Graphics, 2005, 10.1109/CAD-CG.2005.1.

REFERENCES

Chehlarova, T., Stanchev, G. (2001). Formation of skills in students to work with errors in AVITO classes. In: Scientific works of PU “P. Hilendarski”, 38(2), Teaching methodology, 107 – 112.

Dimitrov, J. (2002). Automatic reconstruction from scanned image of mechanical drawing in axonometry, Annual of the University of Mining and Geology “St. Ivan Rilski”, 44 – 45, part III, Mechanization, electrification and automation in mines, Sofia, 93 – 97.

Elias, M. (2012). 3D Model reconstruction from vector perpendicular projections, Scientific Monographs in Automation and Computer Science, 1.

Fang, F. (2014). Algorithms for the Recovery of 3D Objects from 2D Line Drawings, School of Mechanical & Aerospace Engineering, Nanyang Technological University.

Hoang, L. (2020). 3D Solid Reconstruction from 2d Orthographic views, Mixed Reality and Three-Dimensional Computer Graphics, DOI: 10.5772/intechopen.91977.

Idesawa, M. (1973). A system to generate a solid figure from three view, Bulletin of the JSME, 16(92).

Lebamovski, P., Nikolova, M. (2019). An innovative approach to teaching stereometry at school using the StereoMV stereo system, DOI: 10.55630/STEM.2019.0101

Park, H. S., Shiratori T., Matthews I., Sheikh Y. (2010). 3D Reconstruction of a Moving Point from a Series of 2D Projections.

Valkov, M. (2024). Central symmetry on a 3-dimensional board, 10 years of Virtual School Mathematics Classroom, ISBN 978-954-561-636-5.

Valkova, D., Valkov, M. (2024). Using the StruniMa system in technical drawing training, Automation of discrete production, 2, ISSN 2682-9584, mf.tu-sofia.bg/adpmagazine/includes/archive/2024_2.pdf.

Wei, L., Yuanjun H. (2006). 3D model retrieval based on orthogonal projecitons, Computer Aided Design and Computer Graphics, 2005, 10.1109/CAD-CG.2005.1.

Zareva, T. (2016). A model for studying descriptive geometry with dynamic structures for students of architecture and construction, Bulgarian Academy of Sciences, Abstract.

Zareva, T., Chehlarova, T. (2016). Errors when finding a plane section of a body in axonometry and means of overcoming them im. Pedagogical Forum, 3.

INVESTIGATING PROJECTIONS OF 3-DIMENSIONAL SHAPES WITH THE STRUNIMA SYSTEM

Abstract. In the StruniMa system there is a functionality for visualizing square grid in 3D – using it one can find the orthogonal projections of shapes that lie inside the grid or consisting of unit cubes with vertices that coincide with the vertices of the grid. Also there is a part of the system which consists of competitive levels which require finding the third projection when only the first and the second are given.

Keywords: StruniMa; technical drawing; projections; vertices; edges; faces

Dr. Mladen Valkov

Институт по Математика и Информатика

Е-mail: mladen.vulkov@math.bas.bg

strunimaofficial@gmail.com

mlado1992@abv.bg

https://strunima.valkovbg.com/download.html

>> Download the article as a PDF file <<