Kiril Kambushev
ORCID iD: 0000-0001-7884-5626
Bulgarian Air Force Academy “Georgi Benkovski”, Bulgaria
Naiden Chivarov
ORCID iD: 0000-0002-3629-8107
Bulgarian Academy of Sciences, Institute of information and communication technologies, Bulgaria
Martin Kambushev
ORCID iD: 0000-0002-7681-4524
Bulgarian Air Force Academy “Georgi Benkovski”, Bulgaria
https://doi.org/10.53656/adpe-2025.14
Pages 164-172
Abstract. In this report, a study of the properties of the artificial neural networks in the process of voltage regulation of an aviation DC generator has been made. The system’s response to a disturbance expressed in the application of a single step signal will be evaluated. This disturbance will be expressed in a change in the generator rotation speed.
Keywords: PID; neural networks; DC generator; control; regulator
- Introduction
The development of aviation inevitably involves the improvement of aviation equipment, the introduction of new technologies and the design of new systems. Thanks to this, with each new generation of aviation equipment, their capabilities and the range of tasks solved by both manned and unmanned aircraft expand (Kanchev, 2023). On the other hand, all new systems on board the UAV have more and more requirements for the quality of electrical energy.
This is the reason why power supply systems play a major role in determining the capabilities of aircraft. It is inconvenient that the familiar theory of industrial power systems cannot be applied to their study, due to the fact that aviation systems operate in very specific conditions. Some of them are the variable rotation frequency, change in operating temperature, air humidity, mechanical overloads, etc. The wide range of changes in the parameters of the operating conditions of aviation power supply systems leads to a difficult choice of materials used and the design of individual units.
The main source of electricity in small and medium-sized aircraft is the DC generator. The nominal voltage of these generators is 27 V, with a tolerance of ±5%, and the rotation frequency varies from 4000 to 9000 rpm. This sets high requirements for the regulating equipment in order to ensure that high-quality electricity reaches consumers. Increasing the accuracy of voltage regulation provides higher reliability of on-board systems, as well as reducing the mass of the aircraft’s power supply system. This is achieved by more accurate calculation of the network itself; the lower the accuracy of regulation, the larger the cross-sections of the wires must be used.
Various methods are used to increase the accuracy of voltage regulation, combining a high level of the control signal when the controlled signal deviates greatly from the set value, and a decrease in the level of the control signal when approaching the set value. This is achieved through various circuit solutions, which complicate the entire system and reduce its reliability. This report will examine the possibility of an artificial neural network (ANN) being trained to regulate the voltage of an aviation DC generator, using data from a classic PID regulator as a comparison.
- Experiment
The application of artificial neural networks and artificial intelligence in all areas of science today is huge.
This also applies to their application in automatic control systems of both individual systems and entire devices such as cars and airplanes. One of the great advantages of ANN over other automatic control systems is the ability to monitor and manage several processes in parallel. Another great advantage is the high reliability of failure-free operation, which is of particular importance in the management of processes in which the accuracy and continuity of control is of particular importance.
The mathematical model of the artificial neuron was developed in the middle of the last century. With the development of technology, its implementation began for calculating and modeling various mathematical tasks. Nowadays, artificial intelligence is used – a system that has the ability to make decisions on its own. Of course, this is only in limited cases and tasks.
All the advantages of artificial neural networks are combined with some difficulties. One of them is the training of the network itself to perform a specific task. The training itself consists of changing the weights of the connections between individual neurons until a response of the ANN is reached that matches or comes as close as possible to the desired response (Haykin, 2009). This is achieved by seeking to minimize the error – the difference between the ANN response and the real value, and in the training process the following problems may be encountered:
- convergence – choosing small steps will achieve finding the minimum of the function, but this can take a long time and will accordingly lead to an indefinite increase in the training time of the ANN;
- paralysis – this is a condition in which, during ANN training, changing the weights of connections does not lead to actual changes in the ANN response, and this can extend the training time indefinitely. Paralysis occurs during the ANN training process when some of the connections become very large in weight. This leads to the fact that a large part of the neurons with very large argument values will work in the activation function region, where the derivative of the function approaches zero. When calculating the value of the weights, this derivative is used in the formula as a coefficient – the correction value of the weights is proportional to the value of the derivative, then the training process can practically “freeze” and ANN paralysis can occur;
- local minimum – gradient descent along the error surface in the space of synaptic connection weights to a local minimum is used to adjust the weight values in the ANN. However, a local minimum is an acceptable solution in some cases and unacceptable in other cases. Typically, the error surface of a complex ANN is very rough and consists of hills, valleys, and folds in a space of large dimensions. The ANN can fall into a local minimum and not find the global minimum. At the local minimum point, all directions lead up and the ANN cannot get out of it. To overcome this difficulty in training, the number of hidden layers and the number of neurons in the hidden layers are increased, or they are trained several times and then they choose the version of the trained ANN that gives the best results;
- overfitting – high accuracy of the training set can lead to unstable results when testing the ANN. The better an ANN is adapted to certain specific conditions (training data set), the less it is able to generalize and extrapolate. In this case, the ANN models not the function, but the noise present in the training set. This phenomenon is called overfitting. This drawback can be avoided by using a test sample of examples that are used to identify overfitting of the ANN.
One of the most widely used algorithms for solving optimization problems is the Levenberg – Marquardt algorithm (LMA) (Cong & Liang, 2009; Yuan & Wang, 2009). It was developed independently by Kenneth Levenberg and Donald Marquardt around the 1960s and allows solving the problem of minimizing nonlinear functions, which is why it is also known as the method of decreasing least squares. LMA combines the Gauss-Newton algorithm and the gradient descent method to find the minimum of the function under study (Tousif & Sundareswaran, 2014).
For the present study, a two-hidden layer neural network with 14 neurons in each layer was synthesized, shown in fig.1. This choice was made experimentally, as this configuration achieves high network response accuracy and short training time. The simulation of the individual processes was performed using MATLAB/Simulink.
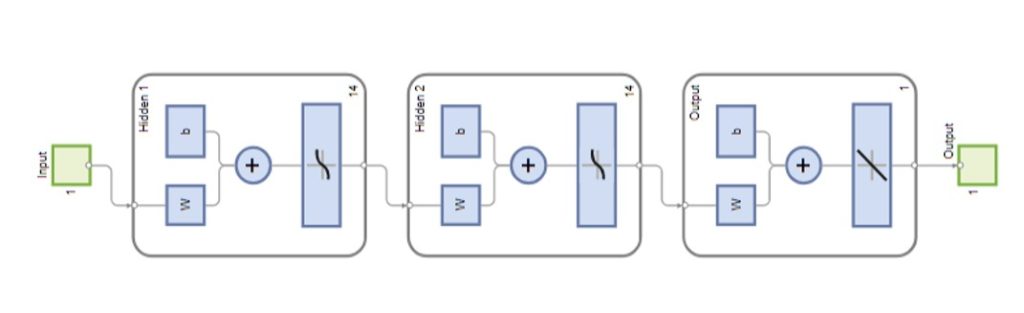
Figure 1. ANN model
An aviation DC generator, the model of which is shown in fig. 2, was chosen as the control object. (Kambushev & Kambushev, 2023). A classical PID controller is used as a basis for comparison and data collection for training the ANN. The ANN will be trained to respond to a disturbance representing a step-wise increase in the generator rotation speed (experiment 1), and then to an increase with a subsequent decrease (experiment 2).
To test the training process of the ANN, data sets containing 1000, 2000, 5000, 8000 and 10000 control values were used to adjust the weights of the connections. During the study, it was found that the optimal number of training data, from those proposed, is 8000, since the accuracy of the ANN response at 8000 and 10000 is the same, but the training time for the latter data set is 15% longer.
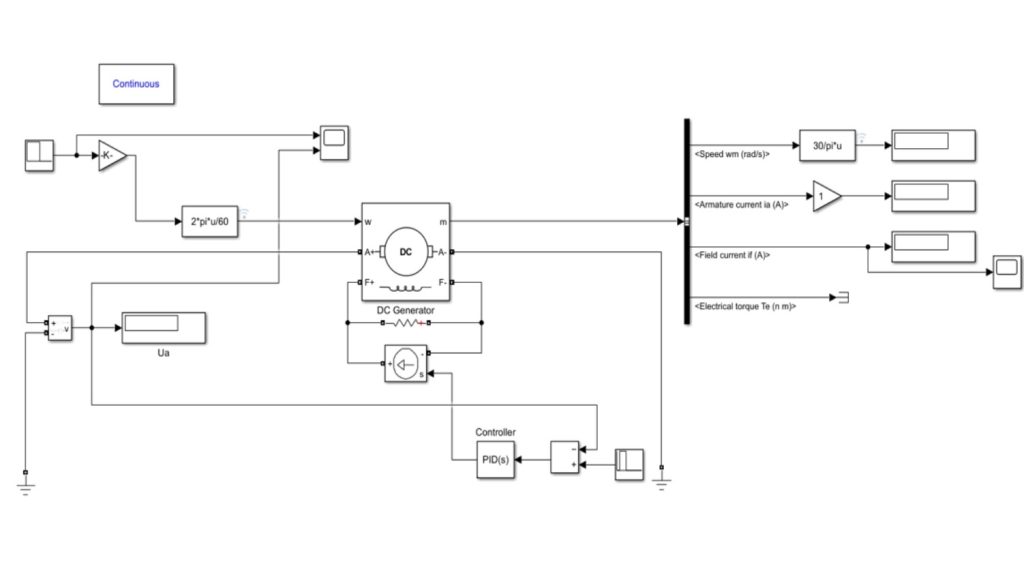
Figure 2. Model of an aviation DC generator
Fig. 3 shows the response of the ANN to a stepwise increase in rotation speed from 4200 to 9000 rpm.
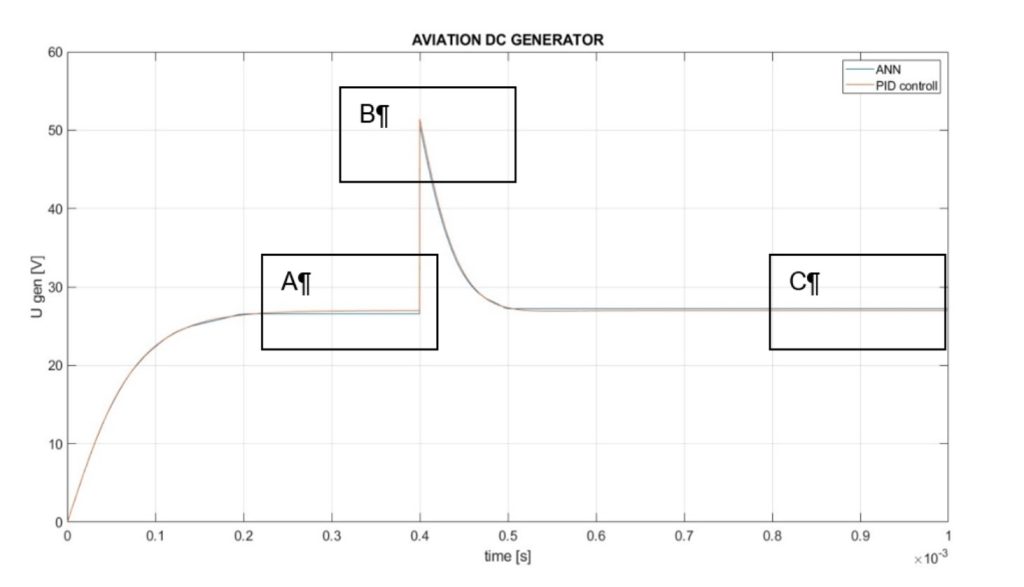
Figure 3. ANN reaction
Fig. 4, 5 and 6 show the marked zones A, B and C. Figure 4 shows that when using the ANN as a voltage regulator, a difference of 0.432 V from the set value is obtained, which is 1.6%. Figure 6, after the transition process is completed, shows that this difference is 0.216V – 0.8%. Figure 5 shows the peak value of the voltage obtained when changing the speed. With the PID regulator it is 51.41 V, and with the ANN it is 50.6 V.
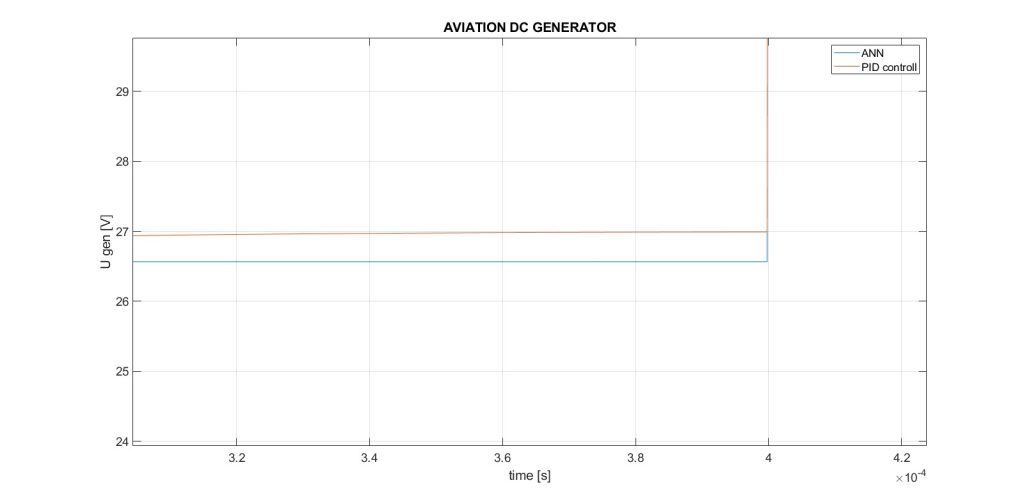
Figure 4. ANN reaction – A
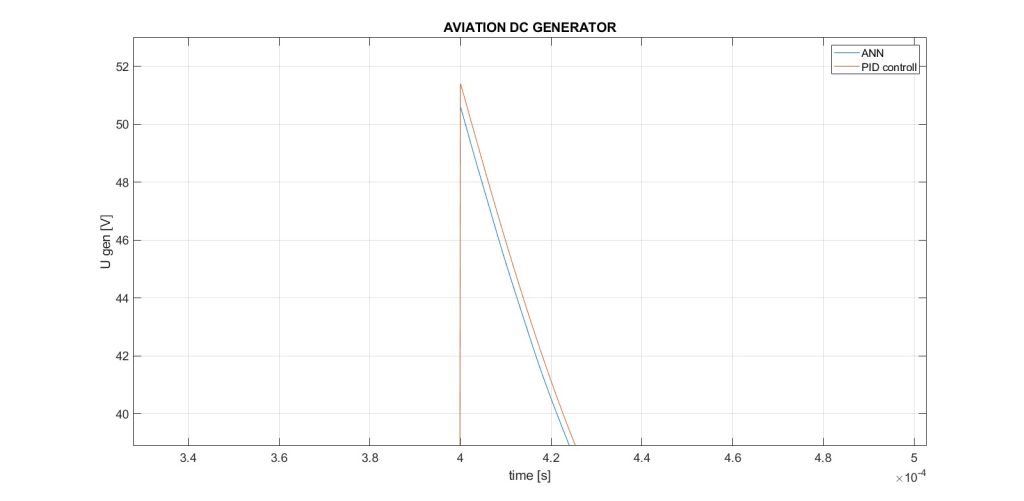
Figure 5. ANN reaction – B
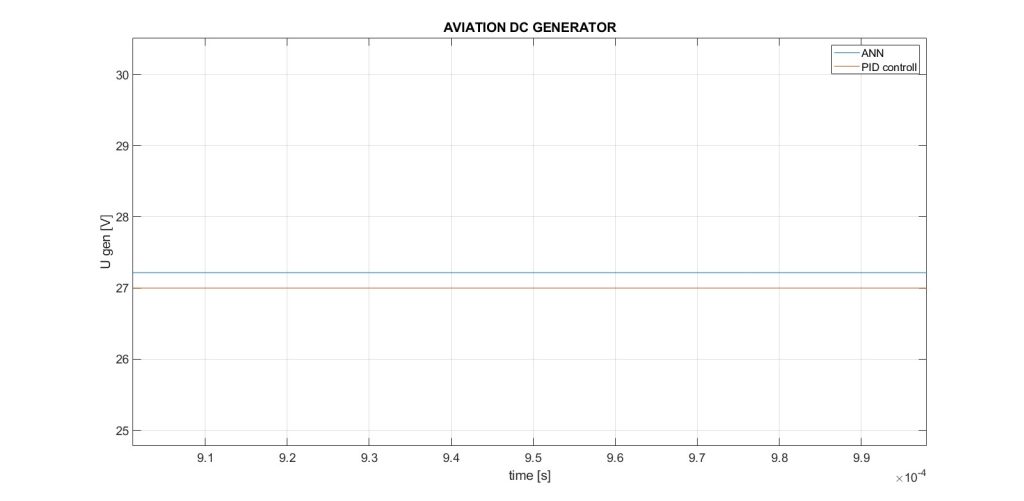
Figure 6. ANN reaction – C
Fig. 7, 8, 9, 10 and 11 show the response of the ANN to a stepwise increase in the generator speed with a subsequent decrease.
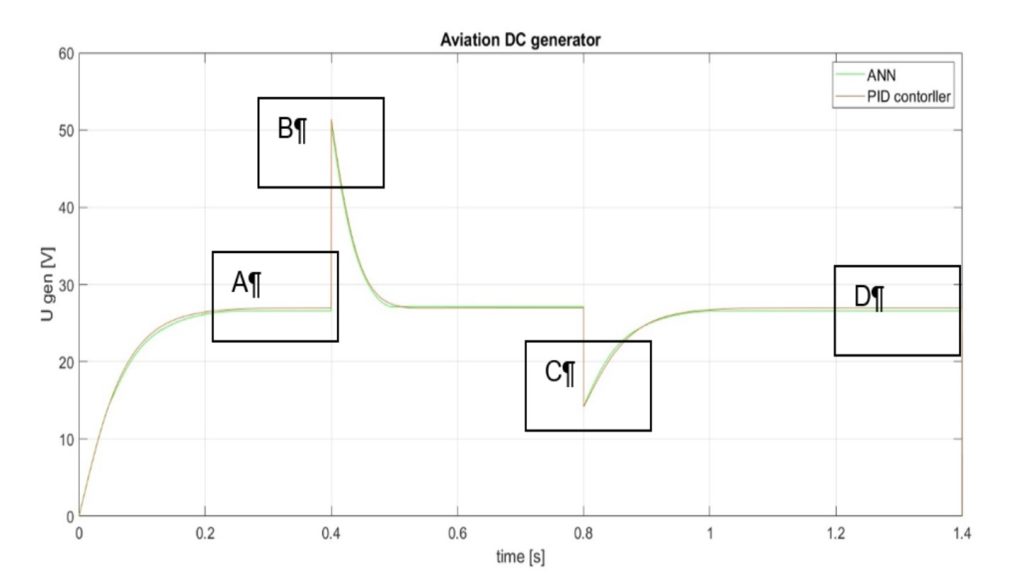
Figure 7. ANN2 reaction
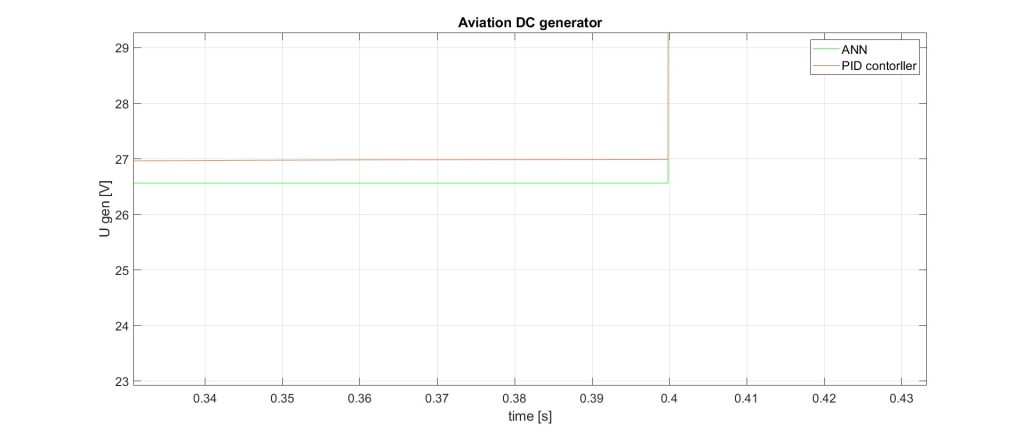
Figure 8. ANN2 reaction – A
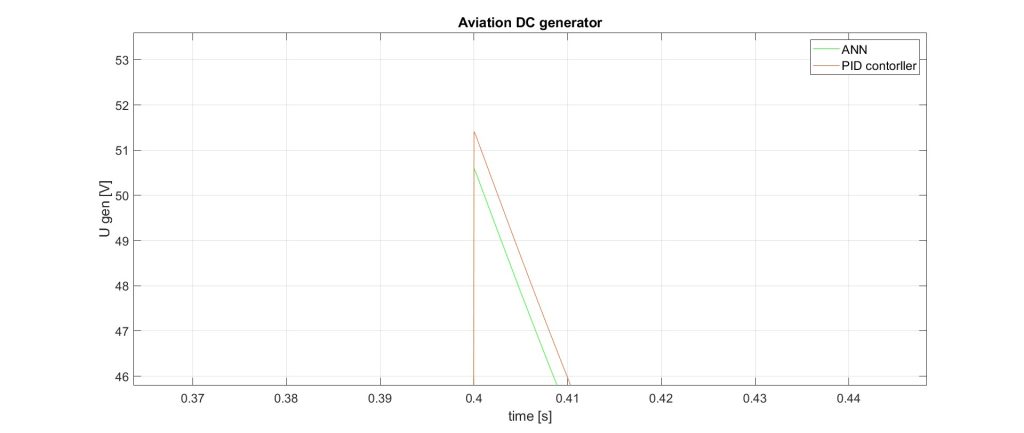
Figure 9. ANN2 reaction – B
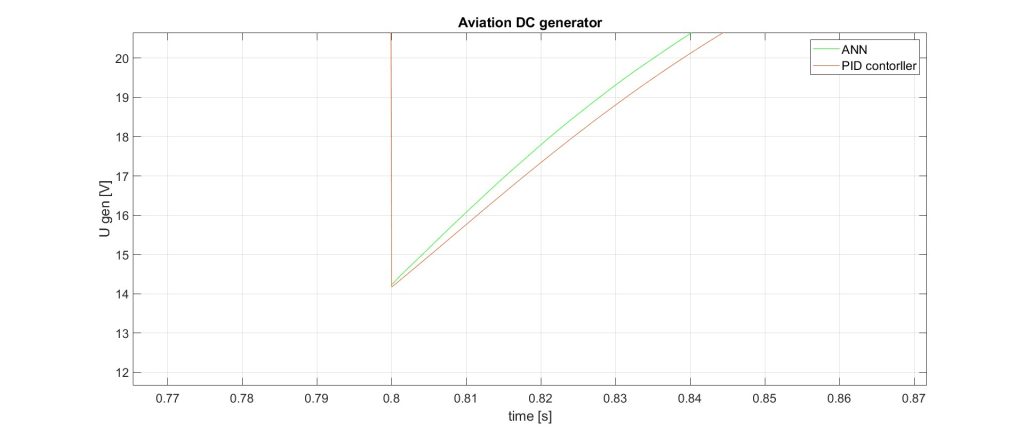
Figure 10. ANN2 reaction – C
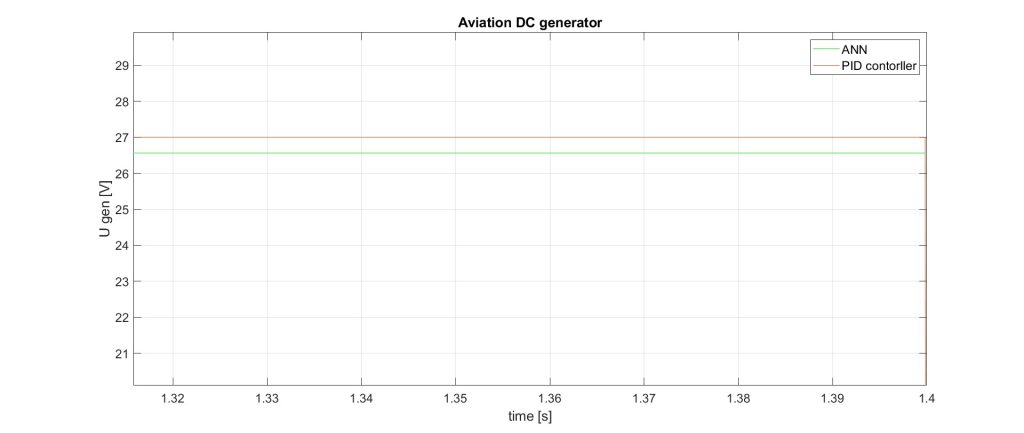
Figure 11. ANN2 reaction – D
- Conclusions
This report explores the possibility of an artificial neural network being trained to perform the functions of a PID controller, with the control object being an aviation DC generator. A two-layer ANN was synthesized, with 14 neurons in each layer. The Levenberg-Marquardt algorithm was used for training. 8000 control values were used for training. The simulation results showed the following:
- experiment 1 – in the established operating mode of the generator, the voltage deviation from the set value of 27V when controlled with the ANN is +0.216V (0.8%) and -0.433V (1.6%). The peak voltage value is 50.6V, which is 0.8V less than when controlled with the PID controller.
- experiment 2 – in the established operating mode of the generator, the voltage deviation from the set value of 27V when controlled with ANN is -0.375V (1.3%) and -0.442V (1.6%). The peak value of the voltage when the speed increases is 50.54V, which is 0.86V less than when controlled with a PID controller, and when decreasing the difference is 0.05 V.
From the research conducted, it can be concluded that ANNs can be used as controllers for aviation DC generators and engines, applicable in both manned and UAV.
Acknowledgement
“The research in this article was carried out in fulfillment of Task 3.1.9. “Construction of a network of autonomous low-powered aerial devices (quadracopters) for control of an urbanized area” by the National Scientific Program “Security and Defense”, adopted by RMS No. 731 of 21.10.2021. and according to Agreement No. D01-74/19.05.2022.“
REFERENCES
Cong, S., Liang, Y. (2009). PID-like neural network nonlinear adaptive control for uncertain multivariable motion control systems. IEEE Transactions on Industrial Electronics, 56(10), 3872 – 3879. https://doi.org/10.1109/TIE.2009.2018433.
Haykin, S. (2009). Neural networks and learning machines (3rd Ed.). Pearson.
Kanchev, N. (2023). Suav-assisted atmospheric research and monitoring systems: current status and perspectives. Bulgarian Air Force Academy’s Annual International Scientific Conference, 31 – 42.
Kambushev, K., Kambushev, M. (2023). Modeling of the Magnetic System of an Aircraft DC Generator. International Conference on Electronics, Engineering Physics and Earth Science (EEPES’2023). https://doi.org/10.1088/1742-6596/2339/1/011001.
Tousif, N., Sundareswaran, K. (2014). Voltage regulation enhancement in a buck type dc dc converter using queen bee evolution based genetical gorithm. IEEE 6th IndiaInternational Conference on Power Electronics (IICPE), 1 – 6. https://doi.org/10.1109/IICPE.2014.7115836.
Yuan, X. F., Wang, Y. N. (2009). Neural networks based self-learning PID control of electronic throttle. Nonlinear Dynamics, 55, 385 – 393. https://doi.org/10.1007/s11071-008-9371-1.


