Arjan Skuka
Ss. Cyril and Methodius University in Skopje (North Macedonia)
Orkun Kozanoğlu
Üsküdar University (Turkey)
Faruk Bulut
Istanbul Esenyurt University (Turkey)
https://doi.org/10.53656/ped2025-4s.09
Abstract. Programming pedagogy deals with methods and principles of teaching and learning computer programming. Teaching nested loops in introductory programming courses (IPCs) is a complex task because it represents the first exposure of beginners to programming logic. To increase significantly students’ comprehension of loops, we introduce a pedagogical method of teaching nested loops. The research was designed as experimental study with posttest experimental and control groups model involving university students. While the experimental group was subjected to the pedagogical method, the traditional method was applied in the control group. To collect the research data, achievement posttest and a questionnaire were developed and applied. The research findings showed clearly the effectiveness of teaching loops by using the pedagogical method. Its advantage over the traditional method was especially reflected at teaching multiple nested loops because their explanation by using the pedagogical method significantly increased the level of logical understanding of this operation which is difficult to comprehend by beginners in programming.
Keywords: teaching programming; learning programming; programming pedagogy; nested loops; pedagogical method
1. Introduction
Programming pedagogy is e very important research area in computer science. It deals with the methods and principles of teaching and learning computer programming, especially in the introductory programming courses (IPCs). A variety of programming pedagogical approaches have been proposed to increase the efficiency of learning computer programming. Mostly, they focus on the tools, paradigms, programming languages and environments used in IPCs (Chetty and Barlow-Jones 2014; Meyer 2003; Porter and Simon 2013; Zingaro, Bailey Lee, and Porter 2013; Hadjerrouit 2008). These approaches have had positive effects in IPCs, but unfortunately they did not solve the problem. Introductory programming remained complex and difficult for majority of students to learn.
Based on our experience in teaching IPCs in C, C++, Java, Pascal, Scheme, Python, Visual Basic at several universities, explaining programming topics in a step-by-step and understandable way is a very important factor in increasing students’ success in IPCs. This way of teaching represents a solid basis for the other student activities in the course: lab exercises, homework, programming projects, solving problems using Online Judges etc. On the other hand, if the topic is explained in less understandable way, it usually frustrates and demotivates students for the required further activities.
To increase significantly the students’ success rates in IPCs, previously mentioned approaches should be complemented with optimal pedagogical explanation methods. How a programming topic is explained is crucial to the level of students’ comprehension of the topic. Being an expert in programming doesn’t make an instructor a good teacher by default.
Definition. Pedagogical explanation method is a well planned and structured sequence of steps to present a programming topic in a concise, clear and understandable way. Recursion, matrix programming operations, nested loops and linked lists are some of the topics that students usually find difficult to understand in IPCs. In this paper we have focused on explanation methods of teaching nested loops (NL). They are usually easy to use for experienced programmers, but they are usually difficult to learn and use by beginners in programming. The purpose of the research was to investigate the effects of two different explanation methods on students’ level of topic comprehension as a result of using a traditional explanation (TE) method and a pedagogical explanation (PE) method.
2. Method
Research design
In this research, we have used an experimental study with posttest control group model aimed at measuring the effects of two different explanation methods on students’ level of topic comprehension. In accordance with this model, control group (CG) and experimental group (EG) were created and experimental lectures using two different explanation methods were conducted.
Research sample
Participants in the experiment were 60 students of Education Faculty attending the Software in Education course, which focuses on programming in Python. Both CG and EG were consisted of 30 students. The distribution of students in the groups was done based on their average grades, insuring that there was no significant difference between the total average grades of students in both groups.
Research instrument and procedure
To collect the data of the study, an achievement test and a questionnaire were developed. After that, we conducted experimental lectures using two different explanation methods in the spring semester of the 2023-24 academic year. NL were taught to students in CG by using a traditional explanation method, while our pedagogical explanation method was used in EG. The survey process was finished by conducting a posttest and a questionnaire to students of both groups.
Data Analysis
Students’ level of a programming topic comprehension can be measured in terms of knowledge level and application level. The achievement posttest contained two programming problems aimed at determining students’ knowledge and application levels of NL, after the experimental lectures were conducted. In addition to the test, we prepared an attitude questionnaire which contained two multiple-choice questions aimed at collecting students’ opinions towards both explanation methods. Students’ answers were measured using a five-point Likert scale.
The quantitative data from the achievement posttest was analyzed using the programming language R. We wrote an R script to read students’ scores in R data frames and analyze them. For analysis purposes we used independent variables t-test and other tools of the language (built-in functions mean, sd, bar plot etc.). The level of statistical significance was taken as 0.05.
3. Explanation methods of teaching NL
In this section, a traditional and a pedagogical explanation method of teaching nested loops are described. We have chosen nested loop problem of average difficulty.
Problem 1: Print a figure with K rectangles of M lines with N stars in each line. Values of K, M and N are red from the standard input in a single line separated by a space.
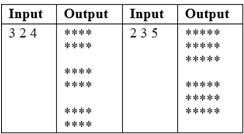
Figure 1. Input/Output samples of Problem 1
3.1. Traditional explanation method
TE method of solving this problem writes and explains directly the solution.
K,M,N = map(int, input().split())
for k in range(K):
for i in range(M):
for j in range(N): print(‘*’,end=“)
print()
print()
K rectangles are selected by changing variable k of the outer loop in the range from 0 to K-1. M lines in each rectangle are selected by changing variable i of the second loop in the range from 0 to M-1. N stars in each line of each rectangle are printed by changing the variable j of the third loop from 0 to N-1. After printing each line output goes to new line. Also, after printing each rectangle output goes to new line. This explanation is quite difficult for beginners to understand.
3.2 Pedagogical explanation method
Step 1. Explain visually solution’s output containing the rectangles of stars produced for the given input values.
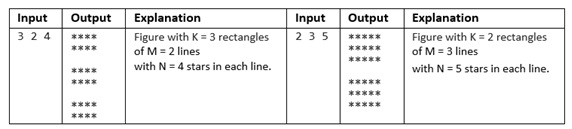
Figure 2. Visual explanation of Problem 1
Step 2. Subproblem. Draw a rectangle of M lines with N stars in each line. Write the two inner nested loops to draw a rectangle, use concrete values for M and N and visualize the output for those values. To make it more clear, counter of number of lines starts with 1 and ends with M. Likewise, counter of number of stars starts with 1 and ends with N.
M – number of lines, N – number of stars, line – counter of lines, i – counter of stars
for line in range(1,M+1):
for i in range(1,N+1): print(‘*’,end=“)
print()

Figure 3. Visual presentation of the subproblem
Step 3. Insert the previously defined two nested loops in an outer loop to draw K rectangles of M lines with N stars each, use concrete values for K, M, N for counters rectangle, line, i and visualize the program output for those values.
K – number of rectangles, M – number of lines, N – number of stars,
rectangle – counter of rectangles, line – counter of lines, i – counter of stars,
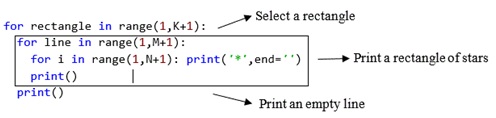
Figure 4. Visual presentation of the solution of Problem 1 using PE method
Algorithm:
- Select a rectangle with 1 ≤ rectangle ≤ K
- Draw a rectangle of M lines with N stars each.
- Print an empty line.
4. Findings and results
4.1. Analysis of the Achievement Posttest Scores
To determine students’ knowledge and application levels of NL after the experimental lectures were conducted, the achievement posttest contained two programming problems. Solutions to each of the problems were weighted with maximum 50% of the total number of points in the test.
− Analysis of Scores of EG and CG in the Achievement Posttest Regarding Students’ Knowledge Level of NL.
To determine students’ knowledge level of NL, the following problem was given in the achievement posttest:
Problem 2: Print a triangle of stars with M lines.

Figure 5. Input/Output samples of Problem 2
Students’ solutions were weighted with maximum 100 points. The obtained findings are given in Table 1.
Table 1. Achievement Posttest Scores of EG and CG Regarding Students’ Knowledge Level of NL
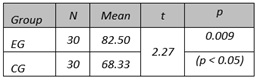
Table 1 shows a significant difference between the scores of the students of EG and CG in the achievement posttest regarding students’ knowledge level of NL, in favor of EG. The mean score of the students in EG (82.50) was 20.73% higher than the mean score of the students in CG (68.33). The obtained t-value (2.27) was larger than the critical value (2.001) and the p-value (0.009) was smaller than 0.05.
− Analysis of Scores of EG and CG in the Achievement Posttest Regarding Students’ Application Level of NL.
To determine students’ application level of NL, the following problem was given in the achievement posttest:
Problem 3: Print a figure of M triangles with N lines in each triangle. Values of M and N are red from the standard input in a single line separated by a space.
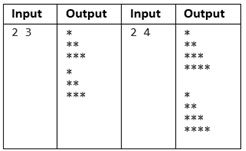
Figure 6. Input/Output samples of Problem 3
Students’ solutions were weighted with maximum 100 points. The obtained findings are given in Table 2.
Table 2. Achievement Posttest Scores of EG and CG Regarding Students’ Application Level of NL
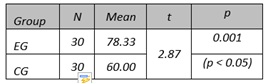
Table 2 shows a significant difference between the scores of the students of EG and CG in the achievement posttest regarding students’ knowledge level of NL, in favor of the experimental group. The mean score of the students in EG (78.33) was 30.56% higher than the mean score of the students in CG (60.00). The obtained t-value (2.87) was larger than the critical value (2.00) and the p-value (0.001) was smaller than 0.05.
− Analysis of the Overall Scores of EG and CG in the Achievement Posttest.
To determine the overall success of the students in the achievement posttest, we summed the points gained for the solutions to programming problems for each student and computed the mean scores for both EG and CG. The obtained findings are given in Table 3.
Table 3. Achievement Posttest Overall Scores of EG and CG
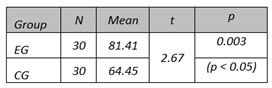
The mean overall score of students in EG (81.41) as 26.36% higher than the mean overall score of the students in CG (64.45). The obtained t-value (2.67) was larger than the critical value (2.03) and the p-value (0.003) was smaller than 0.05.
4.2. Attitude Questionnaire Results and Analysis
Based on the fact that the students in EG obtained significantly higher scores than the students in CG in the achievement posttest, we wanted to determine opinions of both EG and CG students towards both explanation methods. In order to do that, it was necessary for the students in each group to be familiar with the explanation method used in the other group. So, we presented the TE method to students in EG and PE method to students in CG. The following two questions were addressed to students in the attitude questionnaire:
Question1. “Pedagogical explanation method of teaching NL is more efficient compared to traditional explanation method in terms of students’ level of topic comprehension”.
Question2. “Pedagogical explanation method of teaching NL is more understandable to students compared to traditional explanation method”.
Students’ answers to both questions were measured using a common five-point Likert scale (Strongly Disagree, Disagree, Neutral, Agree, Strongly Agree). The obtained findings are given in Table 4.
Table 4. Questionnaire Results Regarding Students’ Attitude Towards PE and TE Methods
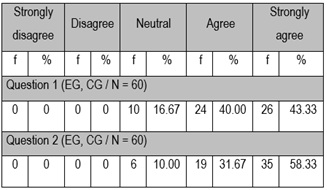 In response to the first question 43.33% of the students strongly agreed, 40% agreed, 16.67% were neutral and none disagreed. In response to the second question 58.33% of the students strongly agreed, 31.67% agreed and only 10% were neutral and none disagreed. Based on the answers to the first question, a total of 83.33% of students found PE method more efficient than TE method, in terms of students’ level of topic comprehension. The answers to the second question clearly showed that 90% of the students found the PE method more understandable than TE method. None of the 60 students found the TE method more efficient or understandable than PE method.
In response to the first question 43.33% of the students strongly agreed, 40% agreed, 16.67% were neutral and none disagreed. In response to the second question 58.33% of the students strongly agreed, 31.67% agreed and only 10% were neutral and none disagreed. Based on the answers to the first question, a total of 83.33% of students found PE method more efficient than TE method, in terms of students’ level of topic comprehension. The answers to the second question clearly showed that 90% of the students found the PE method more understandable than TE method. None of the 60 students found the TE method more efficient or understandable than PE method.
5. Conclusion and discussion
Table 1 Showed than the mean score of the students in EG was 20.73% higher than the mean score of the students in CG. This significant difference in favor of the EG showed that the pedagogical explanation method of teaching NL was more efficient than the traditional explanation method, in terms of students’ knowledge level of NL.
Table 2 revealed than the mean score of the students in EG was even 30.56% higher than the mean score of the students in CG. This significant difference in favor of the EG showed that the pedagogical explanation method of teaching NL was much more efficient than the traditional explanation method, in terms of students’ application level of NL.
Table 3 indicated that the mean overall score of the students in EG was 26.36% higher the than mean overall score of the students in CG. This significant difference in favor of the EG showed that our pedagogical explanation method was more efficient than the traditional explanation method in terms of the overall students’ achievements in the posttest.
Students’ feedbacks on both explanation methods presented in Table 4, clearly reflected that majority of students (86.67%) considered the pedagogical explanation method of NL more efficient and understandable than the traditional explanation method. None of the students found TE method more efficient or understandable than PE method.
Finally, on a more general level, the results of this research suggested that pedagogical explanation methods should be developed and used for other topics in IPCs that students usually find difficult to understand, like recursion, linked lists, matrix programming operations etc. Using these methods can be a very important factor in significantly increasing students’ success in introductory programming courses.
REFERENCES
CHETTY J. & BARLOW-JONES, G., 2014. Novice Students and Computer Programming: Toward Constructivist Pedagogy. Mediterranean Journal of Social Sciences, vol. 5, no. 14, pp. 240 – 250. Available from: https://doi.org/10.5901/mjss.2014.v5n14p240.
FARES, S.C., & FARES, M.A., 2014. A Redesigned Pedagogy in Introductory Programming Reduces Failure and Withdrawal Rates by Half. World Academy of Science, Engineering and Technology. International Journal of Social, Management, Economics and Business Engineering, vol. 8, no. 5, pp. 1259 – 1262. Available from: https://doi.org/10.5281/zenodo.1092233
HADJERROUIT, S., 2008. Towards a Blended Learning Model for Teaching and Learning Computer Programming: A case Study. Informatics in Education, vol. 7, no. 2, pp. 181 – 210. Available from: https://doi.org/10.15388/infedu.2008.12.
MASON, R.; COOPER, G. & RAAD, M., 2012. Trends in Introductory Programming Courses in Australian Universities – Languages, Environments and Pedagogy. Proceedings of the 14th Australian Computing Education Conference, Melbourne, Australia, pp. 33 – 42.
MEYER, B., 2003. The Outside-In Method of Teaching Introductory Programming. Proceedings of the 9th IPSJ-SIGSE Symposium on Object-Orientation, Information Processing Society of Japan, pp. 66 – 78.
PORTER, L. & SIMON, B., 2013. Retaining Nearly One-Third more Majors with a Trio of Instructional Best Practices in CS1. ‘SIGCSE 13 Proceeding of the 44th ACM Technical Symposium on Computer Science Education, pp. 165 – 170. Available from: https://doi.org/10.1145/2445196.2445248.
SAELI, M., et al, 2011. Teaching Programming in Secondary School: A Pedagogical Content Knowledge Perspective. Informatics in Education, vol. 10, no. 1, pp. 73 – 88. Available from: https://doi.org/10.15388/infedu.2011.06.
STEPHEN, M., et al, 2012. Choosing Tools of Pedagogy (Case of Program Visualization). Application or Innovation in Engineering & Management, vol. 1, no. 4, pp. 35 – 40. ISSN: 2319 – 4847.
VITKUTE-ADŽGAUSKIENE, D. & VIDŽIUNAS, A., 2012. Problems in Choosing Tools and Methods for Teaching Programming. Informatics in Education, vol. 11, no. 2, pp. 271 – 282. Available from: https://doi.org/10.15388/infedu.2012.15.
ZINGARO, D.; BAILEY LEE, C. & PORTER, L., 2013. Peer Instruction in Computing: the Role of Reading Quizzes. SIGCSE ’13 Proceeding of the 44th ACM Technical Symposium on Computer Science Education, pp. 47 – 52. Available from: https://doi.org/10.1145/2445196.2445216.
Prof. Dr. Arjan Skuka
ORCID iD: 0009-0009-6509-4603
Ss. Cyril and Methodius University
Skopje, North Macedonia
E-mail: arjan.skuka@gmail.com
Dr. Orkun Kozanoğlu, Assist. Prof.
ORCID iD: 0000-0003-1006-4879
Üsküdar University
Istanbul, Turkey
E-mail: orkun.kozanoglu@uskudar.edu.tr
Dr. Faruk Bulut, Assoc. Prof.
ORCID iD: 0000-0003-2960-8725
Istanbul Esenyurt University
Istanbul, Turkey
E-mail: farukbulut@esenyurt.edu.tr
>> Изтеглете статията в PDF <<



