Изграждане на компетенции и компетентности за моделиране в обучението по математика в детската градина и началното училище при студенти бъдещи учители

Мария Темникова

Тракийски университет – Стара Загора

https://doi.org/10.53656/ped2025-4s.04

Резюме. В периода на предучилищното и началното обучение се изгражда базисната математическа подготовка на 3 – 11-годишните деца. Съществен за учебния процес е проблемът за активизиране и стимулиране на познавателната им интереси, включването им в продуктивни практически дейности и развитието в единство на конкретно-образното и абстрактно-логическото им мислене. Един от аспектите за разрешаването му e прилагането на метода моделиране в методическата работа по математика. Ето защо изграждането на професионални компетенции и компетентности относно адекватното му използване при преподаване на математическото съдържание е значимo за студентите бъдещи детски и начални учители. Изследването е лонгитюдинално и в хода на провеждането му е конструиран и апробиран функционално-технологичен модел за теоретична и практическа подготовка. В статията са представени някои от теоретичните постановки, въз основа на които са изградени и аспекти от методическата работа с различни видове модели, които се използват при решаване на математически задачи. Резултатите от емпиричното изследване доказват, че у студентите се изграждат концептуални знания и умения за метода моделиране, който съдейства за ефективна методическа работа при преподаване по достъпен начин на математическите понятия.

Ключови думи: метод; моделиране; методика на обучение по математика

 

 

През последните години реформата във висшето образование е насочена към прилагането на образователен модел, базиран на компетентности, чрез който се реализира обучение, ориентирано към резултатите и допринасящо за изграждането при студентите на умения да прилагат усвоените знания при нови и нестандартни ситуации.

За да прилагат метода моделиране целесъобразно в методическата работа в обучението по математика в детската градина и 1. – 4. клас, те трябва да усвоят съответните теоретични знания, да умеят да планират и провеждат ситуации и уроци, при които многократно да го използват при различни варианти на практически дейности и екипна работа на децата и учениците.

Цел на изследователската работа е да се анализират и систематизират теоретични постановки, свързани с моделирането, въз основа на тях да се изгради модел за теоретико-практическа подготовка на студенти бъдещи учители за използването му в обучението по математика в предучилищното образование и началния етап на основната образователна степен.

При анализа на българска и чуждестранна педагогическа литература се установява, че редица изследователи разглеждат същността на моделите и моделирането,  като метод в обучението (Kirova 2021; Tsankov 2019; Boaler 2001; Griesel 2005; Gravemeijer & Stephan 2002; Pollak 2011).

Според В. Sriraman (Sriraman 2006, pp. 1686 – 1695) „моделът е продукт, а процесът на създаване на физически, символичен или абстрактен модел на ситуация е моделиране“.

H. Doerr и R. Lesh определят моделирането като „концептуални системи…, които се изразяват … и се използват за конструиране, описание или обяснение на поведението на друга(и) система(и) – така че другата система да може да бъде предвидена интелигентно“ (Doerr & Lesh 2003, p. 10).

Моделирането е процес, при който се създава модел. Една от целите му е да се развие умението за обобщение, което е едно от основните умения в обучението по математика¹. Междинният модел в контекста на моделирането като познавателен метод представлява концептуална или формална конструкция, която свързва абстрактните теоретични модели с емпирично наблюдаваните явления. Той редуцира сложността, като представя явленията чрез по-изолирани и управляеми компоненти, което улеснява тяхното разбиране и анализ. Освен това междинният модел позволява адаптация и проверка на хипотези, като създава възможност за емпирична верификация и корекция на теоретичните основи. Характеризира се с гъвкавост и прогностичност, като може да се използва както за анализ на съществуващи процеси, така и за предсказване на бъдещи състояния. В този смисъл той действа като познавателен инструмент, който улеснява взаимодействието между теорията и реалността, подпомагайки разширяването и адаптацията на знанията. В контекста на обучението по математика в детската градина и началното училище, междинният модел представлява познавателен инструмент, който свързва абстрактните математически концепции с конкретния детски опит и интуитивното разбиране. Чрез използването на междинни модели децата постепенно изграждат логически връзки и умения за абстракция. По този начин моделът намалява когнитивната сложност на математическите понятия, като ги представя в достъпна и разбираема форма, което подпомага ефективното усвояване и прилагане на знанията.

В рамките на моделирането като познавателен метод всеки модел е едновременно краен и междинен в зависимост от контекста на изследването. Той е краен, когато изпълнява своята роля за анализиране и разбиране на оригинала. В същото време е междинен, защото получените знания могат да доведат до създаване на по-сложен модел или до по-дълбоко разбиране, което да бъде пренесено върху оригинала или до следващ етап на познание. Този динамичен характер на моделите е ключов за разбирането на моделирането като метод на познание.

При математическото моделиране в предучилищното образование и в начален етап на основната образователна степен се използват математически модели – числови изрази, равенства и др., които повишават абстрактността на обучението.

Според начина на отразяване на математическата същност на разглежданото явление или обект М. Богданова разграничава два вида моделиране: „предметно-образно моделиране – съчетават предметно-образни и абстрактно-логически елементи,  и знаково-символично моделиране – чрез използване на схеми, чертежи, математически записи (изрази, равенства и др.)“ (Bogdanova 1988, pp. 20 – 21).

Математическите модели, като вид знаково моделиране, имат своя специфика, която е резултат от особеностите на математическото познание. Математическата същност на ситуацията е отразена с помощта на математически символи и знаци.

В свое изследване S. Dundar, B. Gokkurt и Y. Soylu (Dundar et al. 2012, pp. 3465 –3470) пишат, че „математическото моделиране има основополагащ аспект относно математическото образование, като включва преобразуването на проблеми от реалния свят в математически форми и е приложим при различните области на математиката и образователните степени“.

По-голямата категория задачи е решаването на всички видове математически проблеми, а математическото моделиране е част от решаването на математически проблеми².

„Математическото моделиране е изкуството или процес на конструиране на математически модел, на математическо представяне на реалността, което улавя, симулира или представя избрани характеристики или поведения на моделираните аспекти от съществуващата реалност“ (Cai et al. 2014, pp. 149 – 150).

Моделирането не е еднократно действие, а адаптивен и динамичен процес. Редица изследователи разглеждат целия процес на моделиране като цикъл: C. Haines и R. Crouch (Haines & Crouch 2007), R. Lehrer и L. Schauble (Lehrer & Schauble 2003), R. Zbiek и A. Conner (Zbiek & Conner 2006) и др. В стандартите на NCTM³ процесът на моделиране също се разглежда като нелинеен процес.

На фигурата е дадена визуализацията на разработения от H. Schupp цикъл на моделиране (Schupp 1989, p. 43).

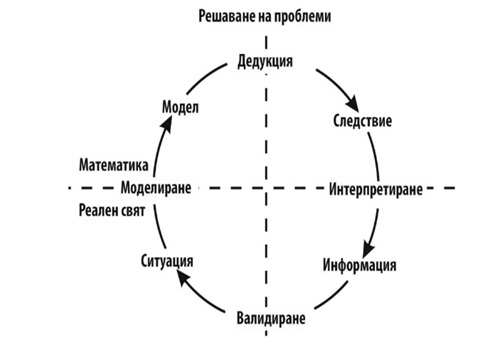
Фигура 1

Той разделя в едно измерение математиката и реалността, а в другото измерение разграничава еднакво проблема и решението. В измерението на проблема наличната информация се възприема, валидира в ситуация, като тя е предварително структуриран математически проблем или математически проблем, свързан с реалния живот. Чрез моделирането се изгражда модел, като в мисловен план се извършват анализ, синтез, абстрахиране, обобщение и дедукция. Извежда се следствието и всеки резултат се интерпретира.

Моделът, стратегиите, технологиите, подходите и методическата система на работа, приложени в изследването, са изградени въз основа на нова динамична модификация (NDM–парадигма), на съответстващите ѝ концептуални модели (Georgieva & Grozdev 2015) и на цикъла на моделиране на H. Schupp.

През последните години в обучението по математика в 1. – 4. група на детската градина и 1. – 4. клас на началото училище широко се използват информационните технологии: електронни учебници, мултимедийни презентации и др. електронни ресурси. В разработения модел те имат роля на образователни технологии, тъй като при познавателната дейност осигуряват възможности за реализиране на определени стратегии. „Принципът за синхронност в контекста на релацията „Математическото моделиране – информационни технологии“ позволява разбирането на редица абстрактни структури в познанието и самопознанието, които трудно се поддават на вербално описание… като математическата интерпретация, видяна чрез един мултимедиен продукт и особено в динамика (присъствие на математическо моделиране)“ (Georgieva & Grozdev 2015, pp. 178 – 180) допринася за вникването в същностните характеристики на математическите понятия.

Изследователската работа протича на три етапа. Първи етап: по време на лекционния курс студентите усвояват теоретични знания за същността на моделирането, видовете модели и значението им за процеса на обучение. Втори етап: по време на семинарните и практическите упражнения студентите прилагат усвоените знания и умения при работа с математическо учебно съдържание, предложено от познавателните книжки и учебните комплекти, одобрени от МОН, разработват свои варианти, работят с модели на различно равнище и с различни функции. Трети етап: по време на хоспитиране и текуща практика студентите прилагат изградените знания и умения относно моделирането в методическата работа в реален процес на обучение в двата етапа.

Въз основа на използваната за разграничаване на различни проблеми таксономия „Структура на математическите задачи“⁴ се изгражда целевият компонент от модела.  Математическите задачи, за които студентите разработват методически варианти, „преминават през три различни фази“. „Първо те се появяват в учебник“ или друго учебно пособие. „След това те се определят от това как учителят представя задачата“ пред обучаемите. При последната фаза „те реално се решават“. Задачите са разработени съобразно класификацията на M. Stein и M. Smith. На „ниско ниво“ са тези на първо ниво – „прости задачи (Memorization Tasks)“, които изискват ниско равнище на когнитивно мислене: трябва да се изкаже правило, факт, и „второ ниво – задачи-процедури без връзки (Procedures without Connections)“, при които се прилага точно определен алгоритъм. Задачите от „високо ниво са на трето и четвърто ниво“ съответно –​​ „задачи-процедури с връзки (Procedures with Connections Tasks)“, изисква се да се решават задачи и представят проблема или отговора по множество начини. Това може да означава „използването на различни видове манипулации или визуални представяния“ и „математически задачи-действия (Doing Mathematics Tasks) – няма известен алгоритъм и е необходимо комбиниране по специфичен начин на алгоритми за решението им, изискват да се изследва, разбере природата на математическите концепции“ (Stein & Smith 1998, pp. 268 – 275).

В процеса на обучение по методика на обучението по математика в детската градина и в 1. – 4. клас студентите усвояват теоретични знания и при тях се формират умения за: модели, които са основен елемент на учебното съдържание, обекти са на познанието и е необходимо да бъдат усвоени от децата и учениците; модели, чрез които се достига до знание за изучаван обект, явление и служат като средство.

В изложението по-долу са описани някои аспекти от методиката на работата при изграждане на понятия за числата, аритметичните действия и някои видове текстови задачи.

При симулационно базирано обучение и работа със задачи-процедури без връзки те разработват методически варианти, при които числата се представят като множества с равен брой елементи, като използват натурални обекти от заобикалящата действителност, изображения на реални обекти, предмети заместители и предварително подготвен индивидуален дидактичен материал. Аналогични методически варианти с по-високо равнище трудност се използват и при изучаване на числата до 10 в 1. клас. Затвърдяват се знанията за числото като количествена характеристика на клас крайни равномощни множества.

Един от методическите варианти, който студентите прилагат, е например във 2. възрастова група при формиране на представи за числото три. Те използват методите моделиране, демонстрация, наблюдение, беседа и на демонстрационно табло нареждат две съвкупности от три на брой пингвини и три на брой риби, които са нагледни опори, които сетивно и непосредствено се възприемат от децата. Чрез похватите налагане или прилагане се установява равномощността на множествата. Следва задача-процедура без връзки – практическа дейност на децата с предварително подготвен индивидуален дидактичен материал. Изграждат се у тях умения самостоятелно да моделират количество от три обекта, като на масичките си подреждат три на брой големи и три на брой малки бели мечки. Чрез манипулативни действия се установява равномощността на елементите в двете групи. Достига се до акцента в методическата работа – математическия смисъл на изобразеното, в математиката общото между количеството в тези 2 групи се означава с числото три. При следващата задача студентите използват електронни ресурси.

Фигура 2

Чрез съотнасяне и съпоставяне децата установяват, че ескимосите и лодките са равни на брой, и свързват със знаковата картина на числото три (модел на числото). Въз основа на предметно-образните представи и чрез абстрахиране отново се насочва вниманието им към общото свойство на съвкупностите.

В 4. подготвителна група пропедевтичното изграждане на знания и умения при децата за аритметичното действие събиране е чрез решаване задачата: На снега има 3 северни елена. Дошъл още 1. Колко общо са елените на снега?. Студентите онагледяват практическа ситуация с мултимедийни ресурси. Тя се моделира на по-високо равнище на абстрактност с помощта на диаграмите на Ойлер-Вен по следния начин:

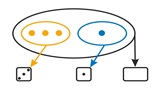
Фигура 3

Децата се подпомагат при анализа и обсъждането на диаграмите. Общият брой елени на снега е очертан с черна линия и в посочената с черна стрелка фигура те записват 4 точки.

В 1. клас при изграждане на понятия у учениците за аритметичните действия събиране и изваждане на числата до 10 също се прилагат идеи за предметно моделиране, като се съдейства за точното и вярно извършване на аритметичните операции, като ситуациите се представят и с помощта на математически модели – числови изрази.

В 1. клас при изучаване на числата до 10, събиране и изваждане с тях се реализира подготвителен етап за работа с текстови задачи за смисъла на действие събиране и изваждане. Елементарна схематична нагледност са схематичните рисунки при следната задача-процедура с връзки:

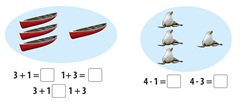
Фигура 4

Схематизацията се осъществява посредством разположението на фигурите една спрямо друга и чрез графично означение на връзките и зависимостите между обектите. Тези рисунки са предметно-образни схеми, модели, които разкриват вътрешни и външни връзки, отношения между изучаваните обекти и явления. Работата със схематичните модели се явява едно от важните средства на абстрахирането и в учебния процес те преди всичко изпълняват функцията на абстрахиране. Чрез видеофайл обектите, участващи в аритметичните операции, се представят в динамика.

Когато при решаването на дадена математическа задача се използват схематични чертежи или т. нар. схематични модели, е налице по-висока степен на обобщеност. Използва се абстрактно-графическа символика. В методическата работа студентите се обучават да построяват схематични модели за различните видове обикновени и за съставните текстови задачи.

При работа с готови схематични модели те изграждат знания и умения у учениците да разчитат моделите, на базата на текста да откриват важни връзки в модела и обратно. Тези чертежи, от една страна, се използват за улесняване разбирането на математическата същност на текстовите задачи, а от друга – за записване на условието ѝ. Например за задачата-процедура с връзки: За края на учебната година четвъртокласници направили изложба с 273 рисунки, които били седем пъти повече от глинените фигурки. Колко общо изделия са направили четвъртокласниците за изложбата? Такъв модел е:

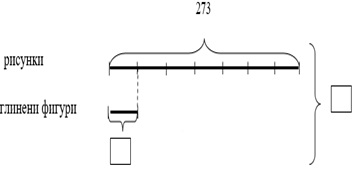
Фигура 5

Студентите разработват методически варианти на работа, при които се разглеждат два спомагателни модела към задача на трето ниво – задача-процедура с връзки, и се установява кой от тях ѝ съответства.

Задача:  През годината за изхранване на животните в зоопарк изразходили 1313 кг зеленчуци и с 202 кг повече месо. Колко общо килограма зеленчуци и месо са изразходвали за храна в зоопарка?

Кой от чертежите отговаря на условието?

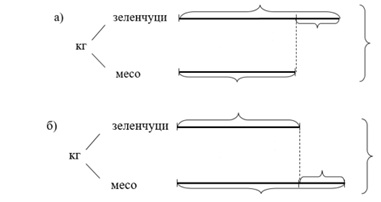
Фигура 6

 На базата на разсъждения учениците откриват верния отговор, като анализът на задачата е скрит в разсъжденията им. Акцент в методическата работа на студентите е насочването на вниманието на третокласниците към определяне на разликата в представянето върху чертежите на пряката и косвената употреба на релациите. При решаването се определят известните и неизвестните компоненти, разкриват се съществените връзки, моделират се основните количествени отношения с помощта на математически модели, изследват се и се съотнасят към дадената задача за решаване.

Изследването е лонгитюдинално и натрупаните емпирични данни са за периода 2014 – 2023 г. със студенти специалност „Предучилищна и начална училищна педагогика“ с извадка с 340 студенти, ОКС „Бакалавър“ и „Магистър“ при Педагогическия факултет на Тракийския университет, Стара Загора. В началния и крайния му етап се установява равнището на знанията и уменията на студентите да: определят какъв вид модел трябва да се използва в обучението по математика и с какви други дидактически средства трябва да се съчетае; изграждат и прилагат различни видове модели в методическата работа при преподаване на конкретно математическо съдържание в 1. – 4. група на детската градина и 1. – 4. клас на началното училище.

Резултатите от емпиричното изследване са систематизирани и анализирани чрез математико-статистически методи за обработка на данни. При входящата диагностика при всички задачи студентите, които са се колебаели, са в диапазона от 42,42% до 50,9%. Най-много грешки са допуснали при задача 4. – 25,9% от тях не са успели да съставят модела или да опишат вярно методическата работа при съставяне на спомагателен модел – чертеж. При задача 3 резултатите им са най-високи – 38,53% от тях са работили вярно.  При изходящата диагностика се установява повишаване равнището на резултатите, като се увеличава процентът на студентите, които вярно работят по всички задачи – в диапазона от 67,94% до 84,71%. Намалява броят на студентите, които работят грешно, и те са от 7,94% до 23,82%. Най-високи резултати са при задачите, свързани с предметно-образното моделиране.

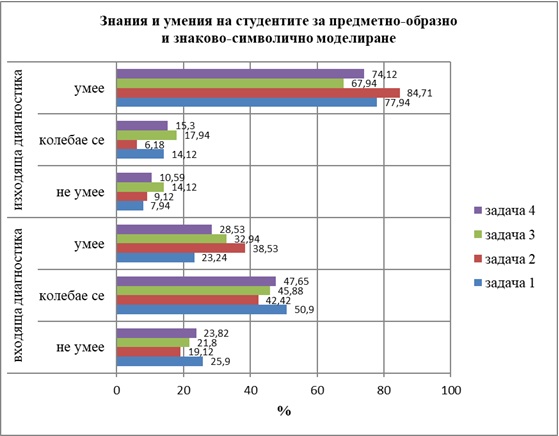
Фигура 7

Изводът от изследователската работа е, че в резултат от прилагането на разработения модел на обучение студентите адекватно използват метода моделиране в методическата работа при решаване на математически проблеми в обучението в 1. – 4. група на детската градина и в начален етап на основната образователна степен съобразно учебното съдържание и познавателното равнище на децата и учениците.

 

БЕЛЕЖКИ

1. OLKUN, S.; ŞAHIN, Ö.; AKKURT, Z.; DIKKARTIN, F.T.; VE GÜLBAĞCI, H. 2009. Modelleme Yoluyla Problem Çözme ve Genelleme: İlköğretim Öğrencileriyle Bir Çalışma. Eğitim ve Bilim. Vol. 34, No. 151. [viewed 28 June 2024]. Available from: https://egitimvebilim.ted.org.tr/index.php/EB/article/view/608.
2. CHAMBERLIN, S. A. 2008. What is problem solving in the mathematics classroom? Philosophy of Mathematics Education, no. 23, pp. 1 – 25. [viewed 3 August 2024]. Available from: https://www.exeter.ac.uk/research/groups/education/pmej/
3. NATIONAL COUNCIL OF TEACHERS OF MATHEMATICS. 1989. Curriculum and evaluation standards for school mathematics. Reston, VA: Author. [viewed 6 July 2024]. Available from: https://www.nctm.org/Standards-and-Positions/NCTM-Standards/
4. STEIN, M. K.; SMITH, M. S. 1998. Mathematical tasks as a framework for reflection: From research to practice. Mathematics Teaching in the Middle School, no. 3, pp. 268 – 275. Copyright 1998 by the National Council of Teachers of Mathematics, Inc. www.nctm.org. [viewed 8 July 2024]. Available from: https://adultedresource.coabe.org/wp-content/uploads/2017/06/Math-Tasks-as-Framework- for-Reflection.pdf .

 

ЛИТЕРАТУРА

БОГДАНОВА, М., 1998. Моделирането в обучението по математика в началните класове на ЕСПУ. Стара Загора: Анастасия Тошева.

ГЕОРГИЕВА, М.; ГРОЗДЕВ, С., 2016. Морфодинамиката за развитието на ноосферния интелект. София: Изток-Запад. ISBN 978-619-152-869-1.

КИРОВА, Г., 2021. Обучението на студенти – бъдещи начални учители, за работа с текстови задачи по математика. София: ВЕДА СЛОВЕНА-ЖГ, ISBN: 978-954-8846-68-4.

ЦАНКОВ, Н., 2019. Обучението в училищното образование. Училищна дидактикa. София: Авангард Прима. ISBN 978-619-239-125-6.

BOALER, J., 2001. Mathematical Modelling and New Theories of Learning. Teaching Mathematics and its Applications, vol. 20, no. 3 [viewed 14 June 2024]. Available from: https://doi.org/10.1093/teamat/20.3.121.

CAI, J.; CIRILLO, M.; PELESKO, J.; BORROMEO FERRI, B.; BORBA, M.; GEIGER, V.; STILLMAN, G.; ENGLISH, L.; WAKE, G.; KAISER, G.; KWON, OH., 2014. Mathematical modeling in school education: mathematical, cognitive, curricular, instructional and teacher education perspectives.  In: LILJEDAHL, P., NICOL, C., OESTERLE, S., & ALLAN, D. (Eds.). Proceedings of the Joint Meeting of PME 38 and PME-NA 36, vol. 1, pp. 145 – 172. Vancouver, Canada: PME. ISSN 0771-100X, ISBN 978-0-86491-361-6, Set ISBN: 978-0-86491-360-9.

DOERR, H.; LESH, R., 2003. Foundations of a models and modeling perspective on mathematics teaching, learning, and problem solving. In: H. DOERR & R. LESH (Eds.). Beyond constructivism: Models and modelling perspectives on mathematics teaching, learning, and problem solving. Lawrence Erlbaum Associates, Publishers.

DUNDAR, S.; GOKKURT, B.; SOYLU, Y., 2012. Mathematical modelling at a glance: A theoretical study. Procedia Social and Behavioral Sciences, no. 46, pp. 3465 – 3470. [viewed 30 August 2024]. Available from: https://doi.org/10/1016/j.sbspro.2012.06.086.

GRAVEMEIJER, K.; STEPHAN, M., 2002. Emergent models as an instructional design heuristic. In: K. GRAVEMEIJER, R. LEHRER, B. OERS, L. VERSCHAFFEL (Eds.). Symbolizing, modeling and tool use in mathematics education. Dordrecht, The Netherlands: Kluwer Academic Publishers.

GRIESEL, H., 2005. Modelle und Modellieren eine didaktisch orientierte Sachanalyse, zugleich ein Beitrag zu den Grundlagen einer mathematischen Beschreibung der Welt. In: H.-W. HENN, & G. KAISER (Eds.). Mathematikunterricht im Spannungsfeld von Evolution und Evaluation. Festschrift für Werner Blum, Hildesheim: div.

HAINES, C.; CROUCH, R., 2007. Mathematical modeling and applications: Ability and competence frameworks. In: W. BLUM, P. L. GALBRAITH, H. HENN, & M. NISS (Eds.). Modelling and applications in mathematics education: The 14th ICMI study. New York, NY: Springer. DOI: 10.1007/978-0-387-29822-1_46.

LEHRER, R.; SCHAUBLE, L., 2003. Origins and evaluation of model-based reasoning in mathematics and science. In: R. LESH, & H. M. DOERR (Eds.), Beyond constructivism: Models and modeling perspectives on mathematics problem solving, learning, and teaching. Mahwah, NJ: Lawrence Erlbaum.

POLLAK, H. O., 2011. What is mathematical modeling? Journal of Mathematics Education at Teachers College, vol. 2, no. 1 [viewed 13 August 2024]. Available from:  https://doi.org/10.7916/jmetc.v2i1.694.

SCHUPP, H., 1989. Applied mathematics instruction in the lower secondary level—Between traditional and new approaches. In: W. BLUM, ET AL. (Eds.), Applications and modeling in learning and teaching mathematics, pp. 37 – 46. Chichester: Ellis Horwood.

SRIRAMAN, B., 2006. Conceptualizing the model-eliciting perspective of mathematical problem solving. In: M. BOSCH (Ed.), Proceedings of the Fourth Congress of the European Society for Research in Mathematics Education (CERME 4). Sant Feliu de Guíxols, pp. 1686 – 1695. Spain: FUNDEMI IQS, Universitat Ramon Llull..

ZBIEK, R., M.; CONNER, A., 2006. Beyond motivation: Exploring mathematical modeling as a context for deepening students’ understandings of curricular mathematics. Educational Studies in Mathematics, no. 69. [viewed 22 July 2024]. Available from: DOI: 10.1007/s10649-005-9002-4.

REFERENCES

BOALER, J., 2001. Mathematical Modelling and New Theories of Learning. Teaching Mathematics and its Applications, vol. 20, no. 3.

BOGDANOVA, M., 1998. Modeliraneto v obuchenieto po matematika v nachalnite klasove na ESPU, pp. 20 – 21. Stara Zagora: Anastasia Tosheva [in Bulgarian].

CAI, J.; CIRILLO, M.; PELESKO, J.; BORROMEO FERRI, B.; BORBA, M.; GEIGER, V.; STILLMAN, G.; ENGLISH, L.; WAKE, G.; KAISER, G.; KWON, OH., 2014. Mathematical modeling in school education: mathematical, cognitive, curricular, instructional and teacher education perspectives.  In: LILJEDAHL, P., NICOL, C., OESTERLE, S., & ALLAN, D. (Eds.). Proceedings of the Joint Meeting of PME 38 and PME-NA 36, vol. 1, pp. 145 – 172. Vancouver, Canada: PME. ISSN 0771-100X, ISBN 978-0-86491-361-6, Set ISBN: 978-0-86491-360-9.

DOERR, H.; LESH, R., 2003. Foundations of a models and modeling perspective on mathematics teaching, learning, and problem solving. In: H. DOERR & R. LESH (Eds.). Beyond constructivism: Models and modelling perspectives on mathematics teaching, learning, and problem solving. Lawrence Erlbaum Associates, Publishers. https://doi.org/10.4324/9781410607713.

DUNDAR, S.; GOKKURT, B.; SOYLU, Y., 2012. Mathematical modelling at a glance: A theoretical study. Procedia Social and Behavioral Sciences, no. 46, pp. 3465 – 3470. [viewed 30 August 2024]. Available from: https://doi.org/10/1016/j.sbspro.2012.06.086.

GRAVEMEIJER, K.; STEPHAN, M., 2002. Emergent models as an instructional design heuristic. In: K. GRAVEMEIJER, R. LEHRER, B. OERS, L. VERSCHAFFEL (Eds.). Symbolizing, modeling and tool use in mathematics education. Dordrecht, The Netherlands: Kluwer Academic Publishers.

GRIESEL, H., 2005. Modelle und Modellieren eine didaktisch orientierte Sachanalyse, zugleich ein Beitrag zu den Grundlagen einer mathematischen Beschreibung der Welt. In: H.-W. HENN, & G. KAISER (Eds.). Mathematikunterricht im Spannungsfeld von Evolution und Evaluation. Festschrift für Werner Blum, Hildesheim: div.

GEORGIEVA, M.; GROZDEV, S., 2016. Morfodinamikata za razvitieto na noosferniya intelekt. pp. 178 – 180. Sofia: Iztok-Zapad [in Bulgarian]. ISBN 978-619-152-869-1.

HAINES, C.; CROUCH, R., 2007. Mathematical modeling and applications: Ability and competence frameworks. In: W. BLUM, P. L. GALBRAITH, H. HENN, & M. NISS (Eds.). Modelling and applications in mathematics education: The 14th ICMI study. New York, NY: Springer. DOI: 10.1007/978-0-387-29822-1_46.

KIROVA, G., 2021. Obuchenieto na student – budeshti nachalni uchiteli, za rabota s tekstovi zadachi po matematika. Sofia: VEDA SLOVENA-ZG [in Bulgarian]. ISBN: 978-954-8846-68-4.

LEHRER, R.; SCHAUBLE, L., 2003. Origins and evaluation of model-based reasoning in mathematics and science. In: R. LESH, & H. M. DOERR (Eds.), Beyond constructivism: Models and modeling perspectives on mathematics problem solving, learning, and teaching. Mahwah, NJ: Lawrence Erlbaum.

POLLAK, H. O., 2011. What is mathematical modeling?. Journal of Mathematics Education at Teachers College, vol. 2, no. 1 [viewed 13 August 2024]. Available from:  https://doi.org/10.7916/jmetc.v2i1.694.

SCHUPP, H., 1989. Applied mathematics instruction in the lower secondary level—Between traditional and new approaches. In: W. BLUM, ET AL. (Eds.), Applications and modeling in learning and teaching mathematics, pp. 37 – 46. Chichester: Ellis Horwood.

SRIRAMAN, B., 2006. Conceptualizing the model-eliciting perspective of mathematical problem solving. In: M. BOSCH (Ed.), Proceedings of the Fourth Congress of the European Society for Research in Mathematics Education (CERME 4). Sant Feliu de Guíxols, pp. 1686 – 1695. Spain: FUNDEMI IQS, Universitat Ramon Llull.

TSANKOV, N., 2019. Obuchenieto v uchilishtnoto obrazovanie Uchilishtna didaktika. Sofia: Avangard Prima [in Bulgarian]. ISBN 978-619-239-125-6.

ZBIEK, R., M.; CONNER, A., 2006. Beyond motivation: Exploring mathematical modeling as a context for deepening students’ understandings of curricular mathematics. Educational Studies in Mathematics, no. 69 [viewed 22 July 2024]. Available from: DOI: 10.1007/s10649-005-9002-4.

 

DEVELOPING STUDENTS – FUTURE TEACHERS’ COMPETENCES
AND COMPETENCIES FOR MODELING IN TEACHING PRE-SCHOOL AND PRIMARY SCHOOL MATHEMATICS

Abstract. During the period of pre-school and Primary school education, 3 – 11-year-old children acquire basic mathematical knowledge. The problem of activating and stimulating students` cognitive interest, their inclusion in productive practical activities, and development in the direction of unity of their concrete-figurative and abstract-logical thinking are essential for the educational process. One aspect of its resolution is the application of the modeling method in the methodology work in mathematics. This is why the development of professional competences and competencies related to its adequate use in teaching mathematical content is so important for future kindergarten and primary teachers. The research was longitudinal, and throughout its implementation, it was the functional-technological model for theoretical and practical student training. The article presents some theoretical concepts on which the lecture course was built. The results of the empirical study proved that students develop conceptual knowledge and skills regarding the Modelling method which facilitates the effective methodology work for understandably teaching the mathematical terminology.

Keywords: method; modelling; methodology of education in mathematics; students-future teachers

 

Dr. Maria Temnikova, Assoc. Prof.
ORCID iD: 0000-0002-4259-8288
Faculty of Education
Trakia University
Stara Zagora, Bulgaria
E-mail: mariya.temnikova@trakia-uni.bg

>> Изтеглете статията в PDF <<