Motion and control of surface-shaping mechatronic neural network

Velizar Vassilev

Technical University of Sofia, Bulgaria

Dobri Komarski

Technical University of Sofia, Bulgaria

Hristiana Nikolova

Technical University of Sofia, Bulgaria

https://doi.org/10.53656/adpe-2025.12

PDF

Pages 138-148

Abstract. This paper presents the motion and control system of a developed surface-shaping mechatronic neural network. The system integrates force sensing resistors that detect user input, allowing the surface to adapt its form based on the intensity and pattern of the applied force. Depending on the input, the shape of the surface can be convex, concave, inclined or any other combined shape as a result of the input data. Focus of this paper is the description of the overall system architecture, including selection, development and integration of hardware components and the control algorithms. The proposed neural network could be applied in different areas while offering an approach to input data driven shape manipulation.

Keywords: mechatronic; neural network; surface-shape; motion; control

 

1. Introduction

The mechanics of the developed surface-shaping mechatronic neural network is based on the manipulators with parallel kinematics (e.g. Stewart Platform) with 3 movable legs (tripods). The neural network consists of 24 tripods that are connected to each other through flexures, force sensing resistors, stepper motors and controller (Fig. 1).

The controller of the system consists of microcontrollers, stepper motor drivers and а microcomputer.

The neural network is activated after a force sensing resistor (FSRs) is pressed. A signal from the resistor is sent to the corresponding microcontroller, which processes the raw data and sends it to the microcomputer.

The microcomputer makes the appropriate calculations and sends commands back to the microcontrollers, which drive the stepper motors, via the stepper motor drivers (Tsokov et al., 2021).

Depend on the size and position of the applied force, the developed software is calculating the new positions of the stepper motors. The result of the stepper motors motion could be various of different surface shapes including concave, convex, inclined or any other combined shape of the surface-shaping network (Rusev et al., 2023). Some of the shapes are exported from the software and shown on Fig. 2.

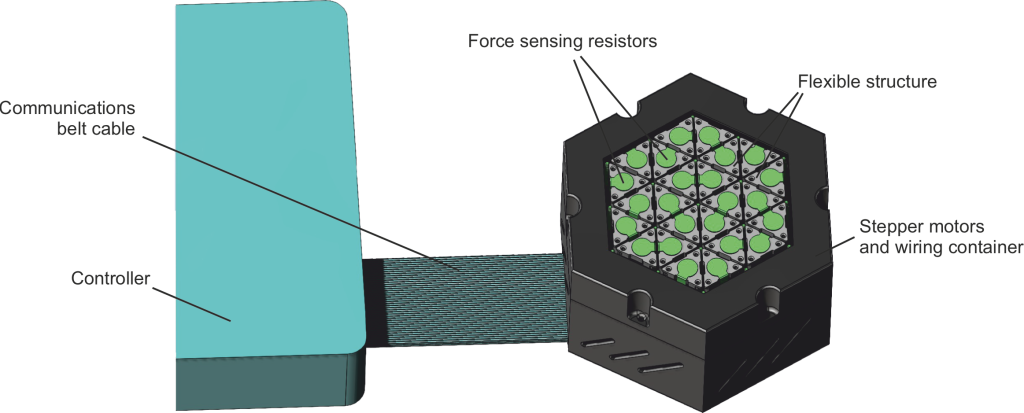
Figure 1. The developed mechanical neural network

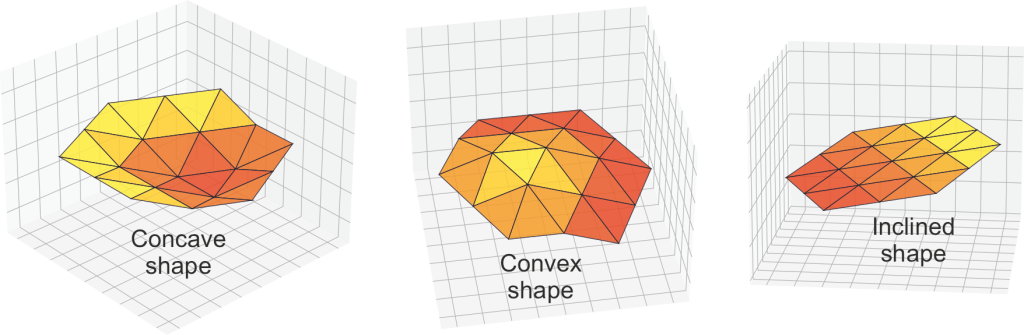
Figure 2. Shapes of the neural network

2. System architecture

The Architecture of the neural network system controller is shown on Fig. 3. The main component of the controller consists of four ESP-WROOM-32 modules, selected for their combination of large number of general-purpose input/output (GPIO) pins, direct USB power supply, built-in USB-to-Serial functionality, as well as the relatively low price and wide support.

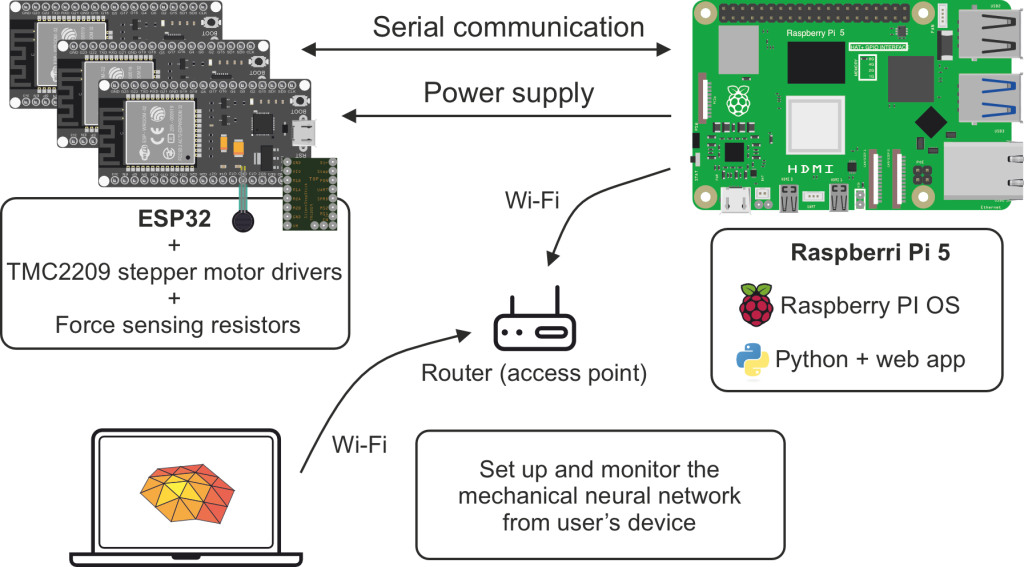
Figure 3. Architecture of the neural networks system controller

Another key component of the controller are the TMC2209 stepper motor drivers, chosen for their energy efficiency, low noise emission, and advanced functionality. A major advantage of the TMC2209 over the other drivers is the diagnostic pin, which enables end-stop detection without the need of additional mechanical limit switches. This significantly simplifies the hardware design of the neural network, reduces the number of required external components, and improves the overall system reliability.

The controller also incorporates force sensing resistors, which measure the applied force on the surface of the system. Each resistor features a circular sensing area with a diameter of 10 mm and a measurement range from approximately 100 g to 10 kg. The sensors are connected to the microcontroller’s GPIOs via a voltage divider, enabling precise conversion of mechanical pressure into an electrical signal for further processing.

The wiring of an ESP32 microcontroller, TMC2209 stepper motor driver and force sensing resistor is illustrated in Fig. 4.

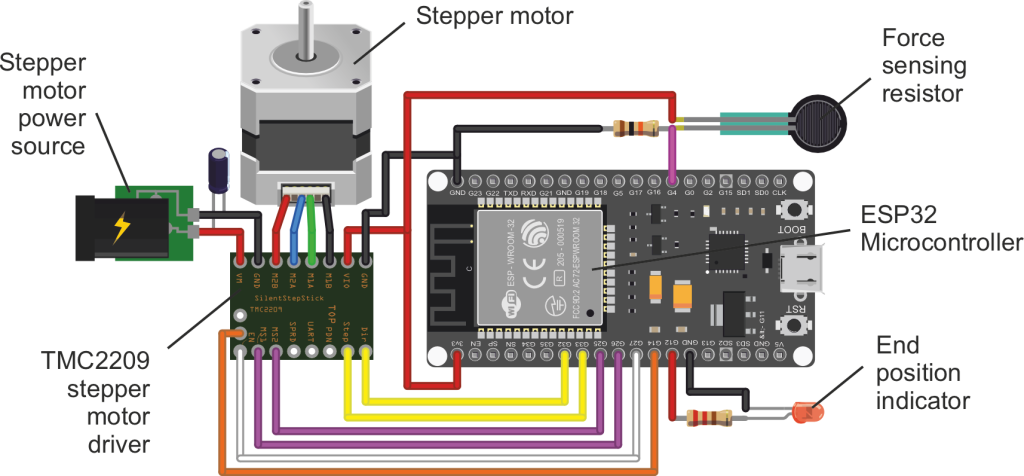
Figure 4. Wiring diagram of the neural network system

The central component of the neural network system is Raspberry Pi 5, which serves as the main computational unit and coordinates the operation of all other components. It was chosen over other alternatives due to its significantly higher computational power, improved processor efficiency, and faster memory compared to previous models. Additionally, its high-speed USB ports ensure reliable and fast communication with the ESP32 modules.

The four ESP32 microcontrollers are connected to it via USB cables, which provide both power and serial communication. This type of communication was chosen over alternatives like I2C or SPI due to its simplicity, reliability over longer distances, and native support in both Raspberry Pi and ESP32, eliminating the need for additional circuitry, complex synchronization and additional power sources for the microcontrollers.

The primary role of Raspberry Pi 5 is to collect and process data from the pressure sensors connected to the ESP32 modules and based on this data, calculate the necessary motions of the stepper motors. Once the calculations are done, the microcomputer sends commands to the ESP32 modules, which then control the drivers to rotate the motors according to the computed values.

Additionally, a dedicated web application has been developed on Raspberry Pi 5 using Python and Flask. It allows users to configure system parameters and monitor the current state of the system in real time. Using the intuitive web interface, the users can access the system from any internet-connected device, enabling remote control and monitoring (Zamkovyi et al., 2023).

3. Control algorithms and software

The control algorithms and software are the core of the neural network’s functionality and they assure the real-time responses to user interactions (Nakov et al., 2025; Trifonov et al., 2022).

The flow chart illustrating the control algorithm is shown in Figure 5.

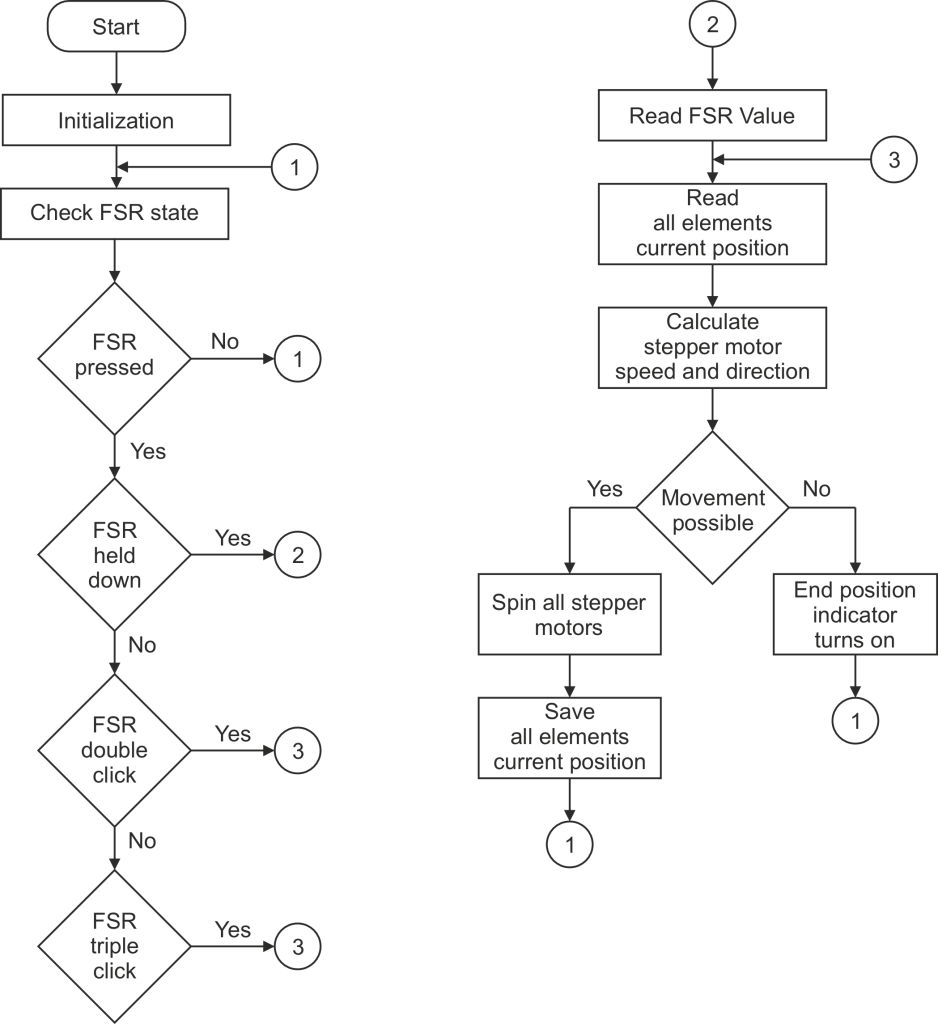
Figure 5. Flow chart of the control algorithm

After the system is started, it the process of initialization by leveling the surface and positioning it to the midpoint of the shafts of the stepper motors (home position). During the initialization process, the program first reads the current coordinates of all points along the z-axis and calculates the centroid C which is reference point for the motion planning and load distribution:

(1)

Subsequently, the elements are moved to the centroid, ensuring that the surface is leveled. This approach prevents potential mechanical damage by minimizing stress on the system components during startup.

Once the initialization is complete, the system waits for activation of any of the force sensor resistors e.g. applied force or pressure on the FSRs. The system recognizes several types of pressure: continuous pressing, double pressing, and triple pressing (similar to a double and triple click with a mouse).

After the type of pressure is identified, the system initiates the corresponding calculations for the movement of the elements.

If the system detects continuous pressure on the FSR, the first step is to determine its force. This is achieved using the 12-bit ADC GPIOs of the ESP32, which convert the pressure force into values ranging from 0 to 4095.

If the value is less than half of the range (F < 2048), the system interprets the pressure as “weak” and initiates the transformation of the surface into a convex shape (Fig. 2).

Conversely, if the value falls within the upper half of the range (F > 2048), the pressure is considered as “strong,” and the system start a transformation to adopt a concave shape (Fig. 2).

Moreover, regardless of the pressure range, the greater the pressure force, the greater the speed of the surface transformation.

In this case the system uses a distance-based motion control algorithm (Gavrylenko et al., 2023; Whitehouse, 2002):

1. When the FSR is pressed, its coordinates are considered as reference point
2. The Euclidean distances d_i from P₀ to all other system elements are calculated:

(2)

3. The number of steps for each stepper motor is proportional to the inverse of (closer elements trigger larger movements):

(3)

where k is a scaling factor.

4. Before execution, the system verifies that the computed steps are within mechanical limits of the system (Tsochev & Sharabov, 2021). If valid, the movement is executed, otherwise, the system doesn’t perform the motion and activates the end position Indicator (Fig. 4) to notify that the maximum position has been reached.

If the system detects a double press on the FSR, it calculates the angle of the current element and then aligns all other elements according to the new position. In the current use case all other components have been aligned with the angle of the pressed component to create an inclined surface profile (Fig. 6).

In this case the system uses a planar alignment algorithm (Dichev et al., 2019; Dichev et al., 2024; Diakov, 2021; Whitehouse, 2002):

1. When the FSR is double pressed, the target plane equation is calculated:

(4)

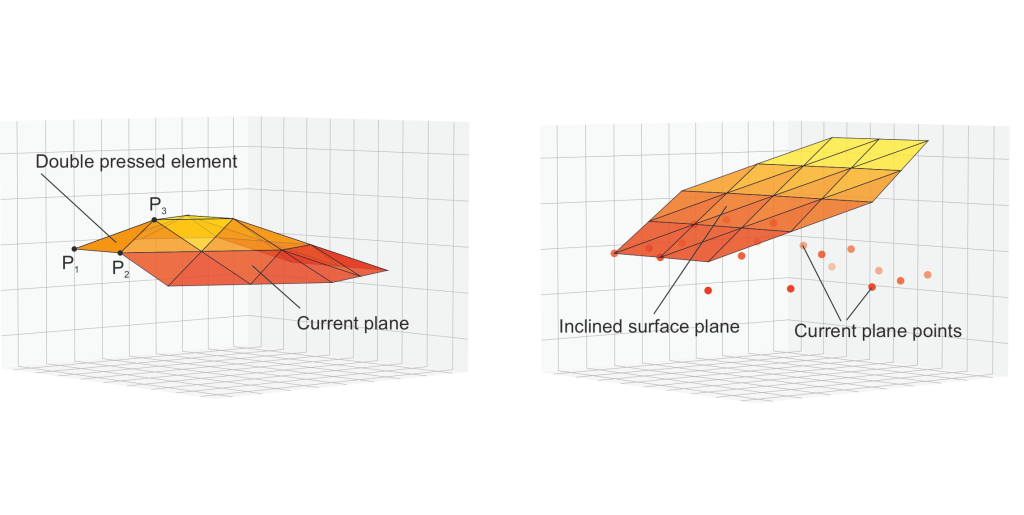
Figure 6. Inclined surface profile using planar alignment algorithm

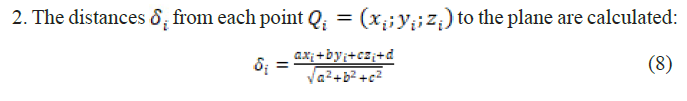
4. The software checks if all steps are within the mechanical bounds and sends commands to the stepper motors.

If the FSR is triple pressed the neural network starts transforms the current shape in a flat surface using the least squares method.

In this case the system uses a least squares plane fitting algorithm (Dichev et al.,  2023; Dichev et al., 2024; Whitehouse, 2002):

The result of the least squares plane fitting is shown on Fig.7.

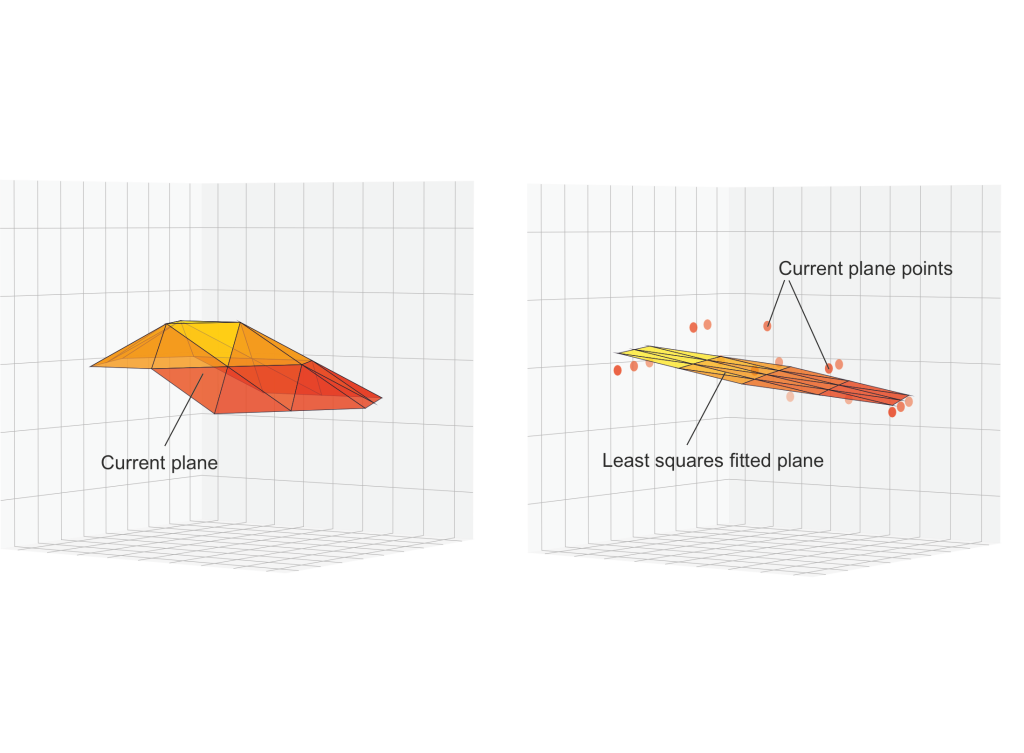
Figure 7. Inclined surface profile using least squares plane fitting algorithm

All the described functions can be changed or adapted to the different applications according to the specific requirements.

In addition, a web application was developed using Flask to provide visualization of the system’s current state and to assure the configuration.

The application can be accessed from any internet-connected device, allowing users to adjust various settings, such as the maximum and minimum movement speed, the increment of movement, the upper and lower position limits along the z-axis, the size of the surface elements, and the displacement magnitude of adjacent elements (Dimitrova et al., 2023; Lothary et al., 2023).

4. Conclusions

The developed surface-shaping mechatronic neural uses force sensing resistors to detect various types of input, allowing the surface to transform into different shapes. The hardware architecture was designed to ensure precision and reliability, with control algorithms effectively translating sensor data into real-time actuation.

Additionally, a web application was developed for visualization and configuration, enabling real-time adjustments from any internet-connected device. The proposed system demonstrates potential for applications in robotics, metamaterials, structural engineering, biomechanics and many more.

 

Acknowledgement

The results in this study were obtained under project No. 251ПР0013-06, funded by the research grant at the Technical University of Sofia. The authors thank the Research and Development Sector at the Technical University of Sofia for their financial support.

 

REFERENCES

Diakov, D. (2021). Measurement of Location Deviations of Flat Surfaces. 31st International Scientific Symposium Metrology and Metrology Assurance. https://doi.org/10.1109/MMA52675.2021.9610893.

Dichev, D., Zhelezarov, I., Karadzhov, T., Madzharov, N., Diakov, D. (2019). Method for Measuring Motion Parameters of Moving Objects. Environment, Technology, Resources, Proceedings of the 12th International Scientific and Practical Conference, 3, 27 – 31. https://doi.org/10.17770/etr2019vol3.4131.

Dichev, D., Zhelezarov, I., Diakov, D., Dicheva, R., Kupriyanov, O., Malakov, I., Anastasov, K., Valkov, S., Petrov, N. (2023). Mathematical Model for Increasing Accuracy when Measuring Linear Quantities in Conditions of External Mechanical Impacts. 33rd International Scientific Symposium Metrology and Metrology Assurance. https://doi.org/10.1109/MMA59144.2023.10317908.

Dichev, D., Diakov, D., Zhelezarov, I., Valkov, S., Ormanova, M., Dicheva, R., Kupriyanov O. (2024). A Method for Correction of Dynamic Errors When Measuring Flat Surfaces, Sensors, 24(16). https://www.mdpi.com/1424-8220/24/16/5154.

Dimitrova, R., Dimitrov, S., Totev, D., Bahchevanov, B. (2023). Electrical Control, Program Code and Experimental Studies of the Gauss Curve in a Specialized Automated Mechatronic System. CIEES 2023 – IEEE International Conference on Communications, Information, Electronic and Energy Systems. https://doi.org/10.1109/CIEES58940.2023.10378762.

Gavrylenko, S., Zozulia, V., Khatsko, N. (2023). Methods for Improving the Quality of Classification on Imbalanced Data. IEEE 4th KhPI Week on Advanced Technology, KhPI Week 2023 – Conference Proceedings. https://doi.org/10.1109/KhPIWeek61412.2023.10312879.

Lothary, D., Tomov, P., Dimitrov, L. (2023). Combination of an ERP System with Other Technological Approaches to Increase Sustainability in Discrete Manufacturing. 2nd International Conference on Electronics, Engineering Physics, and Earth Science, EEPES 2023. https://doi.org/10.1063/5.0195806.

Nakov, O., Lazarova, M., Hinov, N. (2025). Advanced Technologies and Applications in Computer Science and Engineering. Electronics, 14(4), 753. https://doi.org/10.3390/electronics14040753.

Trifonov, R., Nakov, O., Tsochev, G., Nakov, P. (2022). The Use of Intelligent Methods to Protect Industrial Systems. 10th International Scientific Conference on Computer Science, COMSCI 2022 – Proceedings. https://doi.org/10.1109/COMSCI55378.2022.9912603.

Tsochev, G., Sharabov, M. (2021). Artificial intelligence methods used in industry 4.0 in particular industrial control systems. AIP Conference Proceedings, 2333, 070017. https://doi.org/10.1063/5.0041610.

Tsokov, S., Lazarova, M., Aleksieva-Petrova, A. (2021). An evolutionary approach to the design of convolutional neural networks for human activity recognition. Indian Journal of Computer Science and Engineering, 12(2), 499 – 517. https://dx.doi.org/10.21817/indjcse/2021/v12i2/211202145.

Rusev, A., Sharabov, M., Tsochev, G., Trifonov, R. (2023). Artificial intelligence methods suitable for lateral movement detection. AIP Conference Proceedings, 2939, 030002. https://doi.org/10.1063/5.0178852.

Whitehouse, D. (2002). Handbook of Surface and Nanometrology. Taylor & Francis. https://doi.org/10.1201/9781420034196.

Zamkovyi, M., Khatsko, N., Gavrylenko, S., Khatsko, K. (2023). Algorithmic Support for Building a Distributed IoT System in a Cloud Service. IEEE 4th KhPI Week on Advanced Technology, KhPI Week 2023 – Conference Proceedings. https://doi.org/10.1109/KhPIWeek61412.2023.10312994.

 

Assoc. Prof. Velizar Vassilev, PhD
ORCID iD: 0000-0003-1563-2353
Web of Science Researcher ID: X-7785-2018
Technical University of Sofia
Sofia, Bulgaria
E-mail: vassilev_v@tu-sofia.bg

 

Assist. Prof. Dobri Komarski, PhD
ORCID iD: 0000-0002-6838-4608
Web of Science Researcher ID: MFK-2231-2025
Technical University of Sofia
Sofia, Bulgaria
E-mail: dkomarski@tu-sofia.bg

 

Assoc. Prof. Hristiana Nikolova, PhD
ORCID iD: 0000-0003-0484-9709
Web of Science Researcher ID: DKA-0419-2022
Technical University of Sofia
Sofia, Bulgaria
E-mail: hnikolova@tu-sofia.bg